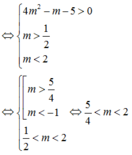Tìm cực trị của hàm số: y=|x2-1|.(x+2)

Những câu hỏi liên quan
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Cho hàm số
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tìm tất cả các giá trị thực của tham số m để hàm số yf(|x|) có 5 cực trị A.
-
10
m
5
4
B.
-...
Đọc tiếp
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Tìm số điểm cực trị của hàm số
y
x
3
−
x
2
−
x
+
1
. A. n4 B. n2 C. n3 D. n1
Đọc tiếp
Tìm số điểm cực trị của hàm số y = x 3 − x 2 − x + 1 .
A. n=4
B. n=2
C. n=3
D. n=1
Tìm số điểm cực trị của hàm số y = x 3 − x 2 − x + 1
A. n = 4
B. n = 2
C. n = 3
D. n = 1
Đáp án C.
Cách 1: Tập xác định: D = ℝ
Ta có:
y = x 3 − x 2 − x + 1 = x 6 − x 2 − x 2 + 1
⇒ y ' = 6 x 5 2 x 6 − 2 x − 2 x 2 x 2 = 3 x 5 − 2 x x 6 − x . x 4 x 6
Ta thấy y' không xác định tại x=0.
- Nếu x > 0 : y ' = 3 x 2 − 2 x 4 − x 3 x 3 = 3 x 2 − 2 x − 1 ; y ' = 0 ⇒ x = 1 .
- Nếu x < 0 :
y ' = 3 x 5 + 2 x 4 − x 3 − x 3 = − 3 x 2 − 2 x + 1 y ' = 0 ⇒ x = − 1
Bảng biến thiên:
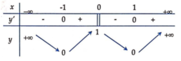
Hàm số đã cho có 3 điểm cực trị.
Cách 2: Đặt t = x , t ≥ 0 . Xét hàm số f t = t 3 − t 2 − t + 1, t ≥ 0 .
Ta có:
f ' t = 3 t 2 − 2 t − 1 ; f ' t = 0 ⇔ t = 0
Bảng biến thiên của hàm số f(t):
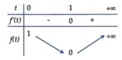
Ta có hàm số y = x 3 − x 2 − x + 1 là hàm số chẵn (đồ thị đối xứng qua trục Oy).
Suy ra bảng biến thiên của hàm số y = x 3 − x 2 − x + 1 :
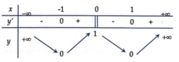
Do đó hàm số y = x 3 − x 2 − x + 1 có 3 điểm cực trị.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số để hàm số
y
4
3
x
3
-
2
(
1
-
sin
a
)
x
2...
Đọc tiếp
Tìm tất cả các giá trị của tham số ![]() để hàm số
để hàm số
y = 4 3 x 3 - 2 ( 1 - sin a ) x 2 - ( 1 + cos 2 a ) x có cực trị.
A.![]()
B. ![]()
C. ![]()
D. ![]()
Tìm giá trị của tham số m để hàm số
a) y = x 3 + (m + 3) x 2 + mx – 2 đạt cực tiểu tại x = 1
b) y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1;
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 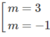
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số α để hàm số
y
4
3
x
3
-
2
(
1
-
s
i
n
α
)
x
2
-
(
1
+
c
o
s
2
α
)
x
có cực trị A.
α
≠
π
2
+
k...
Đọc tiếp
Tìm tất cả các giá trị của tham số α để hàm số y = 4 3 x 3 - 2 ( 1 - s i n α ) x 2 - ( 1 + c o s 2 α ) x có cực trị
A. α ≠ π 2 + k 2 π
B. α ≠ k π
C. α = π 2 + k 2 π
D. α = k π
Tìm cực trị của các hàm số sau: y = x 2 + x - 5 x + 1
TXĐ: R\{-1}
![]()
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để hàm số:
y
1
3
m
x
3
-
(
m
-
1
)
x
2
+
3
(
m
-
2
)
x
+...
Đọc tiếp
Tìm các giá trị của tham số m để hàm số: y = 1 3 m x 3 - ( m - 1 ) x 2 + 3 ( m - 2 ) x + 1 6 đạt cực trị tại x 1 , x 2 thỏa mãn x 1 + 2 x 2 = 1
A. 1 - 6 2 < m < 1 + 6 2 .
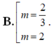
C. m ∈ 1 - 6 2 ; 1 + 6 2 \ 0 .
D. m = 2 .
Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

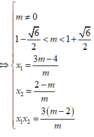

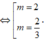
Đúng 0
Bình luận (0)
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn