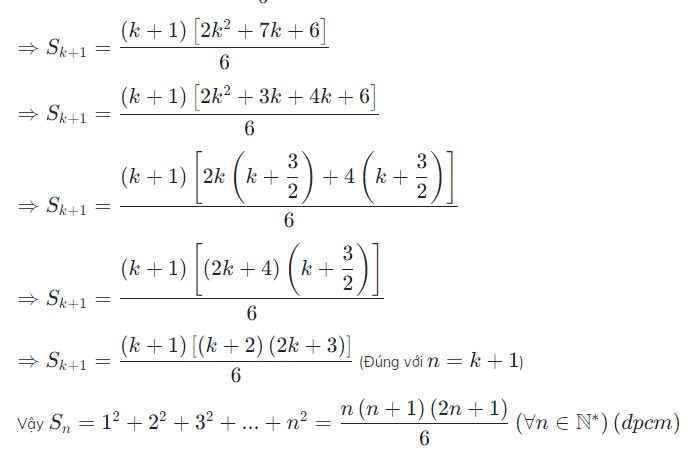Chắc chắn sai đề vì n(n+1) luôn là số lẻ làm sao mà chia hết cho 2 được

Ừ nhỉ,quên mất

Xin lỗi nha!

GIÚP MÌNH VỚI

* Với n = 2 ta có 2 2 + 1 > 2.2 + 3 ⇔ 8 > 7  (đúng).

Vậy (*) đúng với n= 2 .

 * Giả sử với n = k , k ≥ 2  thì (*) đúng, có nghĩa ta có: 2 k + 1   >     2 k   +   3 (1).

* Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:

2 k + 2 > 2 ( k + 1 ) + 3

Thật vậy, nhân hai vế của (1) với 2 ta được:

2.2 k + 1 > 2 2 k + 3 ⇔ 2 k + 2 > 4 k + 6 > 2 k + 5 .

 ( vì 4k + 6 >  4k +  5 >  2k +  5 )

Hay 2 k + 2   >   2   ( k + 1 ) +     3

Vậy  (*) đúng với n = k + 1 .

Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương  ≥ 2

Bước 1: Chứng minh công thức đúng cho n = 1. Khi n = 1, ta có: 1² = 1 = 1 . (1 + 1) . (2 . 1 + 1) / 6 = 1. Vậy công thức đúng cho n = 1.

Bước 2: Giả sử công thức đúng cho n = k, tức là 1² + 2² + ... + k² = k . (k + 1) . (2k + 1) / 6. Ta cần chứng minh công thức đúng cho n = k + 1, tức là 1² + 2² + ... + k² + (k + 1)² = (k + 1) . (k + 1 + 1) . (2(k + 1) + 1) / 6.

Bước 3: Chứng minh công thức đúng cho n = k + 1. Ta có: 1² + 2² + ... + k² + (k + 1)² = (k . (k + 1) . (2k + 1) / 6) + (k + 1)² = (k . (k + 1) . (2k + 1) + 6(k + 1)²) / 6 = (k . (k + 1) . (2k + 1) + 6(k + 1) . (k + 1)) / 6 = (k + 1) . ((k . (2k + 1) + 6(k + 1)) / 6) = (k + 1) . ((2k² + k + 6k + 6) / 6) = (k + 1) . ((2k² + 7k + 6) / 6) = (k + 1) . ((k + 2) . (2k + 3) / 6) = (k + 1) . ((k + 1 + 1) . (2(k + 1) + 1) / 6).

Vậy, công thức đã được chứng minh đúng cho mọi số tự nhiên n khác 0.

tk ủng hộ mk nha mọi người

a:

\(1^2+2^2+3^2+...+n^2=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\left(1\right)\)

Đặt \(S=1^2+2^2+...+n^2\)

Với n=1 thì \(S_1=1^2=1=\dfrac{1\left(1+1\right)\left(2\cdot1+1\right)}{6}\)

=>(1) đúng với n=1

Giả sử (1) đúng với n=k

=>\(S_k=1^2+2^2+3^2+...+k^2=\dfrac{k\left(k+1\right)\left(2k+1\right)}{6}\)

Ta sẽ cần chứng minh (1) đúng với n=k+1

Tức là \(S_{k+1}=\dfrac{\left(k+1+1\right)\cdot\left(k+1\right)\left(2\cdot\left(k+1\right)+1\right)}{6}\)

Khi n=k+1 thì \(S_{k+1}=1^2+2^2+...+k^2+\left(k+1\right)^2\)

\(=\dfrac{k\left(k+1\right)\left(2k+1\right)}{6}+\left(k+1\right)^2\)

\(=\left(k+1\right)\left(\dfrac{k\left(2k+1\right)}{6}+k+1\right)\)

\(=\left(k+1\right)\cdot\dfrac{2k^2+k+6k+6}{6}\)

\(=\left(k+1\right)\cdot\dfrac{2k^2+3k+4k+6}{6}\)

\(=\dfrac{\left(k+1\right)\cdot\left[k\left(2k+3\right)+2\left(2k+3\right)\right]}{6}\)

\(=\dfrac{\left(k+1\right)\left(k+2\right)\left(2k+3\right)}{6}\)

\(=\dfrac{\left(k+1\right)\left(k+1+1\right)\left[2\left(k+1\right)+1\right]}{6}\)

=>(1) đúng

=>ĐPCM
b: \(A=1\cdot5+2\cdot6+3\cdot7+...+2023\cdot2027\)

\(=1\left(1+4\right)+2\left(2+4\right)+3\left(3+4\right)+...+2023\left(2023+4\right)\)

\(=\left(1^2+2^2+3^2+...+2023^2\right)+4\left(1+2+2+...+2023\right)\)

\(=\dfrac{2023\cdot\left(2023+1\right)\left(2\cdot2023+1\right)}{6}+4\cdot\dfrac{2023\left(2023+1\right)}{2}\)

\(=\dfrac{2023\cdot2024\cdot4047}{6}+\dfrac{2023\cdot2024}{1}\)

\(=2023\left(\dfrac{2024\cdot4047}{6}+2024\right)⋮2023\)

\(A=\dfrac{2023\cdot2024\cdot4047}{6}+2023\cdot2024\)

\(=2024\left(2023\cdot\dfrac{4047}{6}+2023\right)\)

\(=23\cdot11\cdot8\cdot\left(2023\cdot\dfrac{4047}{6}+2023\right)\)

=>A chia hết cho 23 và 11

\(A=405^n+2^{405}+17^{37}\left(n\in N\right)\)

\(\Rightarrow A=\overline{.....5}+2^{4.101}.2+17^{4.9}.17\)

\(\Rightarrow A=\overline{.....5}+\overline{.....6}.2+\overline{.....1}.17\)

\(\Rightarrow A=\overline{.....5}+\overline{.....2}+\overline{.....7}\)

\(\Rightarrow A=\overline{......4}\)

Vì chữ số tận cùng của \(A\) là \(4\)

Nên \(A=405^n+2^{405}+17^{37}\) không chia hết cho \(10\)

\(\Rightarrow dpcm\)