15,abc:a,bc=12,1

Những câu hỏi liên quan
Cho tam giác ABC:A=90 độ, B=60 độ,BC=4cm.Tính AB
-Gọi D là trung điểm BC.
-△ABC vuông tại A có AD là trung tuyến ứng với cạnh huyền BC.
\(\Rightarrow AD=BD=CD=\dfrac{1}{2}BC\)
\(\Rightarrow\)△ABD cân tại A mà \(\widehat{B}=60^0\)\(\Rightarrow\)△ABD đều.
\(\Rightarrow AB=BD=\dfrac{1}{2}BC\Rightarrow AB=2\left(cm\right)\)
Đúng 1
Bình luận (0)
Tìm abc:a,b x c,c x a,bc = ab,cabc.cần gấp giúp ha!!!
Cho tam giác ABC:A= 90°,trên tia đối của tia CA, CB lần lượt lấy M,N:AC=CM,BC=CN
a)CM:tam giác ABC=NMC
b)CM:AB=MN
c)CM :MN song song AB
d)cm:MN vuông góc AC e)CM:BM=AN
f)cm:BM SONG SONG NA
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 70 độ, góc B = 50 độ.
So sánh các cạnh của tam giác ABC:
A. AC >BC>AB B. AC>AB>BC C. BC>AB>AC D. AB>AC>BC
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)=180^0-\left(70^0+50^0\right)=180^0-120^0=60^0\)
\(\widehat{A}>\widehat{C}>\widehat{B}\left(70^0>60^0>50^0\right)\)
\(=>BC>AB>AC\)
=> Chọn C
Đúng 1
Bình luận (0)
cho 3 điểm ABC:a ) Gỉa sử AB=2cm, BC=3cm,CA=5cm. Hãy chứng tỏ ABC thẳng hàng. b)Gỉa sử AB=2cm;BC=3cm;CA=4cm.Hãy chứng tỏ ABC không thẳng hàng
cho tam giác ABC có BN là đường trung tuyến G là trọng tâm của tam giác ABC:
a) chứng minh rằng :
BG=2GN
b)kẻ đường AG cắt BC tại M. Chứng minh rằng M là trung điểm của BC
a: Xét ΔABC có
BN là trung tuyến
G là trọng tâm
=>BG=2/3BN
=>BG=2GN
b: Vì G là trọng tâm của ΔABC
nên M là trung điểm của CB
Đúng 0
Bình luận (0)
Cho tam giác ABC:
a) Xác định các điểm M, N, P thỏa mãn: \(\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA} \)
b) Biểu thị mỗi vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {BC} ,\overrightarrow {BA} \)
c) Chứng minh ba điểm M, N, P thẳng hàng
a) Ta có:
+) \(\overrightarrow {MB} = \dfrac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\dfrac{{BC}}{{MB}} = 2\)
\( \Rightarrow M\) nằm ngoài đoạn thẳng BC sao cho \(MB = \dfrac{1}{2}BC\)
+) \({\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \dfrac{1}{4}\overrightarrow {AB} }\)
\( \Rightarrow N\) thuộc đoạn thẳng AB và \(NB=\dfrac{{1}}{{4}} AB\)
+) \(\overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0 \)
\( \Rightarrow P\) là trung điểm của CA
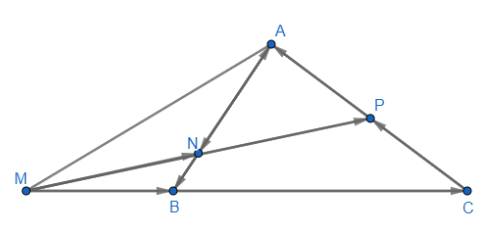
b) \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} \)
\(\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}\)
c) Ta có:
\(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ;\) \(\overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \)
\( \Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN} \)
Vậy \(M,N,P\) thẳng hàng
Đúng 0
Bình luận (0)
tam giác ABC có AB + BC = 20,3 cm ;BC + AC = 12,1 cm ;AC + AB = 12 cm .Tính độ dài cạnh AB
/12,1 nhân x + 12,1 nhân 0,1/ =12,1



















