Cho Tam giác ABC có 3 đường trung tuyến AM,BN,CP đồng qui tại trọng tâm G. Chứng minh MA<MP+MN
Những câu hỏi liên quan
1) tam giác ABC có các đường trung tuyến BD và CE bằng nhau . chứng minh rằng tam giác ABC là tam giác cân.
2)cho tam giác ABC cân ở A , AB=34cm , BC =32cm , và 3 trung tuyến AM , BN , CP đồng quy tại trọng tâm G
a) chúng minh AM vuông góc với
b) tính độ dài AM , BN ,CP (làm trong kết quả đến chữ số thập phân thứ 2)
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
Đúng 1
Bình luận (0)
Cho tam giác ABC có các đường trung tuyến AM, BN, CP trọng tâm G. Gọi K là trung điểm của GB
Chứng minh rằng các cạnh của tam giác GMK bằng 1/3 các trung tuyến tam giác ABC
Nêu cách dựng tam giac ABC khi biết đọ dài 3 đường trung tuyến AM, BN, CP
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
\(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
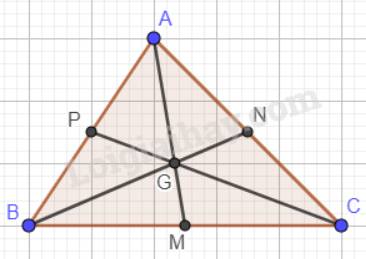
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm G. Chứng minh:
a) SAGP = SPGB = SBGM = SMGC = SCGN = SNGA;
b) Các tam giác GAB, GBC và GCA có diện tích bằng nhau
a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên SAGP = SPGB
Tương tự, ta có: SBGM = SMGC và SCGN = SNGA.
Vì G là trọng tâm DABC Þ AG = 2GM.
Þ SBGM = 1 2 SABG Þ SBGM = SAGP = SPGB.
Chứng minh tương tự, ta suy ra được:
SAGP = SPGB = SBGM = SMGC = SCGN = SNGA
b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6 SABC, từ đó suy ra ĐPCM.
Đúng 0
Bình luận (0)
cho tam giác ABC có trọng tâm G #đường trung tuyến AM : BN ; CP
CM 3(AM+BN+CP)<2(AB+BC+AC
Bài 7 : Cho tam giác ABC cân tại A ,AB = 34cm BC = 32cm và 3 trung tuyến AM , BN CP đồng quytại trung tâm G
A) chứng minh AM ^ BC
b) Tính đọ dài AM BN CP . ( làm tròn kết quả đến số thập phân thứ 2 )
bài 8 : cho tam giác ABC có 2 trung tuyến AM và BN vuông góc với nhau tại G . Chứng minh BC^2 + CA ^2 = 5AB^2
Mình cần gấp các bạn làm nhanh giúp mình ^^
Minh cảm ơn
Cho tam giác ABC có AM, BN, CP là 3 đường trung tuyến, G là trọng tâm. Biết AM=6cm, GB=6cm, PG=1,5cm. Tính AG, MG,BN,CP,GC.
Cho Tam giác ABC với ba đường trung tuyến AM , BN , CP và trọng tâm G .Chứng minh rằng
a, AM < ( AB + AC )
b, ( AB + AC + CA ) < AM + BN + CP < AB + BC + CA
Cho tam giác ABC có các trung tuyến AM, BN, CP cắt nhau tại trọng tâm G. Trên tia AM lấy điểm D sao cho G là trung điểm của AD.CMR: Các đường trung tuyến của tam giác BGD=1/2 các cạnh của tam giác ABC.
Mk cần gấp ạ.