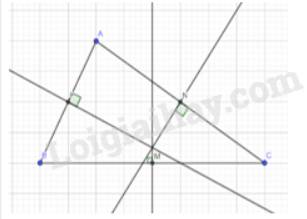
Cho tam giác ABC: M, N, P là trung điểm của BC, CA, AB; O là giao điểm của 3 đường trung trực; các đường cao AD, BE, CF cắt nhau tại H; I, K, R là trung điểm của HA, HB, HC. Chứng minh rằng I, K, R, M, N, P, D, E, F cùng thuộc 1 đường trong ơ-le

Những câu hỏi liên quan
Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC.
Câu 1. Cho tam giác ABC. Gọi O là giao điểm của ba đường trung trực của tam giác ABC. Gọi M, N, P lần lượt là hình chiếu O trên các cạnh AB, BC, CA. Biết AB > BC > CA. Khi đó:
cho tam giác ABC có M , N , P lần lượt là trung điểm của AB , BC , CA . Chứng minh tam giác MNP đồng dạng tam giác ABC
1) Cho tam giác ABC , AB < AC. AH là đường cao; M,N,P lần lượt là trung điểm của AB , BC , CA
a) C/m MP là đường trung trực của AH
b) So sánh chu vi tứ giác MPNH và chu vi tam giác ABC
2) Cho tam giác ABC , H là trực tâm , O là giao điểm 3 đường trung trực. M là trung điểm BC. C/m OM = 1/2 AH
1. Cho tam giác ABC, trung tuyến AM. GỌi I là trung điểm của AM, CI cắt AB ở K. Chứng minh AB = 3AK
2. Cho tam giác ABC không cân, đường cao AH gọi M,N,P theo thứ tự là trung điểm của AB,BC,CA. Chứng minh M,P,N,H là hình thang cân
Cho M (0; 2), N (1; 0), P (−1; −1) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Phương trình đường thẳng AB của tam giác ABC là: A.
y
−
2
x
+
3
B.
y
2
x
+
3
C.
y
...
Đọc tiếp
Cho M (0; 2), N (1; 0), P (−1; −1) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Phương trình đường thẳng AB của tam giác ABC là:
A. y = − 2 x + 3
B. y = 2 x + 3
C. y = − 2 x – 3
D. y = 2 x – 1
Giả sử MN: y = a x + b
Ta có N thuộc MN 0 = a . 1 + b ⇔ a = − b
M thuộc MN 1 = a . 0 + b ⇔ b = 2 ⇔ a = − 2 ⇒ b = 2
Do đó MN: y = − 2 x + 2
Vì M, N lần lượt là trung điểm của các cạnh BC, CA của tam giác ABC nên MN là đường trung bình của tam giác ABC MN // AB
Suy ra AB có dạng: y = − 2 x + b ’ ( b ’ ≠ 2 )
Vì P là trung điểm của AB nên AB đi qua P (−1; −1 )
⇔ − 1 = − 2 ( − 1 ) + b ’ ⇒ b ’ = − 3 ( t / m )
Vậy AB: y = − 2 x – 3
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
cho tam giác abc, biết ab=bc=ca= 3cm, vẽ đường tròn tâm C, bán kính 1, 5 cm, cắt các cạnh BC, CA theo thứ tự ở M và N.
a, điểm M có phải trung điểm của BC ko?
b, điểm N có phải trung điểm của CA ko?
c, Gọi giao điểm AM và BN là I. Chứng tỏ điểm I là điểm nằm trong tam giác ABC.
Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
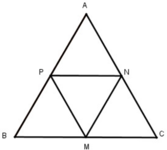
Ta có: M là trung điểm của BC
N là trung điểm của AC nên MN là đường trung bình của Δ ABC ⇒ MN = 1/2 AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của △ ng bình của △ ABC ⇒ NP = 1/2 BC
Mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy △ MNP đều
Đúng 1
Bình luận (0)
Cho tam giác ABC, gọi M,N,P theo thứ tự là trung điểm của AB, BC, CA. Tính cu vi của tam giác MNP biết AB =8cm , BC=12cm, AC=10cm
cho tam giác ABC. Trên các cạnh BC,CA,AB lần lượt lấy ba điểm phân biệt M,N,L . chứng minh rằng nếu LN//BC,MN//AB, LM //AC thì M,N,L lần lượt là trung điểm các cạnh của tam giác ABC