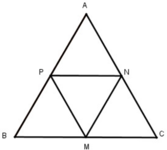
Ta có: M là trung điểm của BC
N là trung điểm của AC nên MN là đường trung bình của Δ ABC ⇒ MN = 1/2 AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của △ ng bình của △ ABC ⇒ NP = 1/2 BC
Mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy △ MNP đều
Cho tam giác đều ABC có diện tích là S. Các điểm D,E,F theo thứ tự thuộc các cạnh AB, BC, CA sao cho \(AD=\frac{1}{3}AB\), \(BE=\frac{1}{3}BC\), \(CF=\frac{1}{3}CA\). Gọi M,N,P lần lượt là giao điểm của AE với CD, AE với BF, BF với CD.
a/ Chứng minh tam giác MNP là tam giác đều.
b/ Tính diện tích của tam giác MNP theo S
Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
1.Cho tam giác ABC. Vẽ bên ngoài tam giác ABC các tam giác đều ABD và BCE. Gọi M, N, P là trung điểm AC, BD, BE. Chứng minh tam giác MNP đều
2.Cho tam giác ABC có I là giao điểm các tia phân giác các góc B và C. Gọi M là trung điểm của BC. Biết góc BIM=90 độ và BI =2IM
a)Tính góc BAC
b)Vẽ IH vuông góc với AC( H thuộc AC). Chứng minh BA = 3IH
Cho tam giác ABC, ở miền ngoài tam giác ta dựng các tam giác đều ABD và BCE . Gọi M,N,P,lần lượt là trung điểm của AC , BD ,BE . Chứng minh tam giác MNP là tam giác đều
Cho tam giác ABC. O là điểm cách đều 3 cạnh của tam giác. Trên cạnh BC lấy điểm M sao cho BM = BA, trên cạnh CB lấy điểm N sao cho CN = CA. Gọi D, E, F lần lượt là hình chiếu của O trên BC, CA, AB. Chứng minh rằng :
a) NE = MF
b) Tam giác MON cân
1 ) Cho tam giác ABC. Vẽ các Tam giác đều ABM và ACN ra phía ngoài tam giác ABC. Gọi D ; E ; F lần lượt là trung điểm của BC ; AM ; AN
Chứng minh : Tam giác DEF đều
2) Cho tam giác ABC và M tùy ý trong tam giác. Gọi D ; E ; F thứ tự trung điểm BC ; CA ; AB. Gọi H ; I ; K thứ tự là điểm đối xứng của M qua D ; E ; F
Chứng minh : AH ; BI ; CK đồng quy tại 1 điểm.
Bài 1. Cho điểm M nằm trong tam giác đều ABC. Chứng minh rằng MA, MB, MC là độ dài ba cạnh của một tam giác. Bài 5. Cho hình thang cân ABCD (AB k CD). AC cắt BD tại O. Gọi E, F, G lần lượt là trung điểm của BC, OA, OD. Biết rằng tam giác EF G đều. Chứng minh rằng AOB, COD cũng là các tam giác đều.
Bài 5. Cho hình thang cân ABCD (AB k CD). AC cắt BD tại O. Gọi E, F, G lần lượt là trung điểm của BC, OA, OD. Biết rằng tam giác EF G đều. Chứng minh rằng AOB, COD cũng là các tam giác đều.
cho tam giác ABC. vẽ phía ngoài tam giác ABC 2 tam giác đều ABD và BCE. gọi M;N;P lần lượt là trung điểm của AC;BD;BE. chứng minh tam giác MNP đều
Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
