Lời giải

Các tỉ số lượng giác của góc β là:

mik nhầm nhé

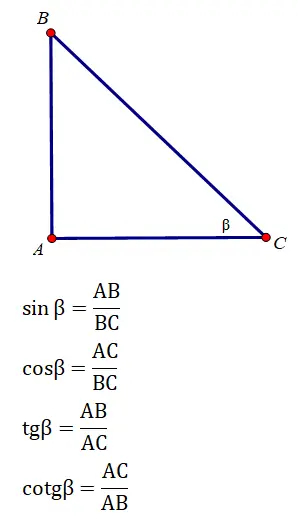
Theo pitago thì BC= căn 2a^2 = căn 2 . a

Khi đó sinB = a/căn 2 . a = căn 2

cosB = sinB = căn 2

tanB = a/a = 1

cotB = tan B = 1

Vậy ta có : ...

xong

\(\tan B=\sqrt{2}\Leftrightarrow\dfrac{\sin B}{\cos B}=\sqrt{2}\Leftrightarrow\sin B=\sqrt{2}\cos B\\ \sin^2B+\cos^2B=1\Leftrightarrow3\cos^2B=1\\ \Leftrightarrow\cos B=\sqrt{\dfrac{1}{3}}=\dfrac{\sqrt{3}}{3}\\ \Leftrightarrow\sin B=\dfrac{\sqrt{6}}{3}\\ \Leftrightarrow\left\{{}\begin{matrix}\sin C=\cos B=\dfrac{\sqrt{3}}{3}\\\cos C=\sin B=\dfrac{\sqrt{6}}{3}\end{matrix}\right.\\ \cot C=\tan B=\sqrt{3};\tan C=\dfrac{1}{\cot C}=\dfrac{\sqrt{3}}{3}\)

Xét ΔABC vuông tại A có 

\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{1}{2}\)

nên \(\widehat{C}=30^0\)

hay \(\widehat{B}=60^0\)

Xét ΔBAC vuông tại A có 

\(\sin\widehat{C}=\cos\widehat{B}=\dfrac{1}{2}\)

\(\cos\widehat{C}=\sin\widehat{B}=\dfrac{\sqrt{3}}{2}\)

\(\tan\widehat{C}=\cot\widehat{B}=\dfrac{\sqrt{3}}{3}\)

\(\cot\widehat{C}=\tan\widehat{B}=\sqrt{3}\)

Bài 1:

a) Ta có:

\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)

\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)  

b) Áp dụng Py-ta-go ta có: 

\(BC^2=AB^2+AC^2=6^2+15^2=261\)

\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)

Bài 2: 

\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)