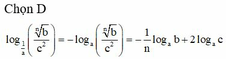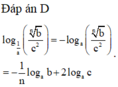Nếu a là 1 số thực và-1<a<1 so sánh a^2 với 1

Những câu hỏi liên quan
Xác định tính đúng sai của mỗi mệnh đề sau:
a) Nếu \(2a - 1 > 0\) thì \(a > 0\) (a là số thực cho trước).
b) \(a - 2 > b\) nếu và chỉ nếu \(a > b + 2\) (a, b là hai số thực cho trước).
a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”
Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.
b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”
Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.
Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.
Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.
Đúng 0
Bình luận (0)
Nếu n là số nguyên dương; b, c là số thực dương và a 1 thì
log
1
a
b
a
c
2
A.
1
n
log
a
b
-
1
2
log
a
c...
Đọc tiếp
Nếu n là số nguyên dương; b, c là số thực dương và a > 1 thì log 1 a b a c 2
A. 1 n log a b - 1 2 log a c
B. n log a b - 2 log a c
C. 1 n log a b - 2 log a c
D. - 1 n log a b + 2 log a c
log 1 a b a c 2 = - log a b a c 2
= - 1 n log a b + 2 log a c
Đáp án cần chọn là D
Đúng 0
Bình luận (0)
Nếu n là số nguyên dương; b, c là số thực dương và a 1 thì
log
1
a
b
n
c
2
bằng A.
1
n
log
a
b
-
1
2
log
a
c
B.
n...
Đọc tiếp
Nếu n là số nguyên dương; b, c là số thực dương và a > 1 thì log 1 a b n c 2 bằng
A. 1 n log a b - 1 2 log a c
B. n log a b - 2 log a c
C. 1 n log a b + 2 log a c
D. - 1 n log a b + 2 log a c
Nếu n là số nguyên dương; b, c là số thực dương và a 1 thì
log
1
a
(
b
n
c
2
)
bằng
Đọc tiếp
Nếu n là số nguyên dương; b, c là số thực dương và a > 1 thì log 1 a ( b n c 2 ) bằng
![]()
![]()
![]()
![]()
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z1-i thì A. . B. . C. . D.
Đọc tiếp
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z=1-i thì
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Nếu 1/a - 1/b = 1 và a, b là các số thực khác 0 và 2a + 3ab - 2b khác 0. Giá trị của biểu thức P = ( a - 2ab - b) / (2a + 3ab - 2b) là
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
. Nếu
z
1
−
i
và
z
1
là hai nghiệm của phương trình thì
a
−
b
−
c
bằng (a, b, c là số thực). A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Nếu \(\frac{1}{a}-\frac{1}{b}=1\) và a,b là các số thực khác 0 và 2a +3ab-2b khác 0. Giá trị của biểu thức (a-2ab-b)/(2a+3ab-2b) là
Ta có
\(\frac{a-2ab-b}{2a+3ab-2b}=\frac{\frac{1}{b}-2-\frac{1}{a}}{\frac{2}{b}+3-\frac{2}{a}}=\frac{-1-2}{3-2}=-3\)
Đúng 0
Bình luận (0)
ta có \(\frac{1}{a}-\frac{1}{b}=1\)\(\)
\(\frac{b-a}{ab}=1\)
\(b-a=ab\)
\(a-b=ab\)
thay vào rồi tính
Đúng 0
Bình luận (0)
Viết 5 số 1;2;3;4;5 lên bảng. Ta thực hiện phép thay thế các số này theo quy luật: Ở mỗi bước, nếu có 2 số a và b nào đó thỏa mãn \(a-b\ge2\) thì xóa hai số này và viết thêm vào hai số a-1 ; b+1. Hỏi ta có thể thực hiện được tối đa là mấy bước như trên.