Từ Phương trình hoành độ giao điểm sẽ tìm được tọa độ của A ( x1,y1) và B (x2 , y2)

Bạn Vẽ hình . Gọi M là hình chiếu của A trên Ox , N là Hình chiếu của B trên Ox . tiếp theo bạn tính lần lượt các diện tích sau.:

1. S tam giác AMO vuông tại M

2. S tam giác BNO vuông tại N 

3. S Hình Thang  AMNB .

=> S tam giác AOB = S Hình thang AMNB -  ( S tam giác AMO + S tam giác BNO)

1) \(\left\{{}\begin{matrix}\left(d_1\right):y=2x\\\left(d_2\right):y=-\dfrac{1}{2}x+5\end{matrix}\right.\)

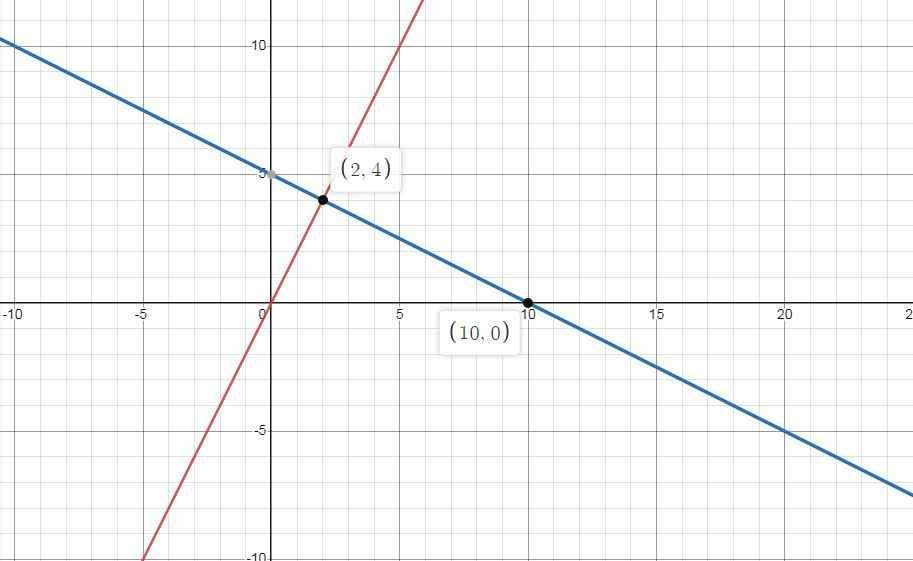
2) Theo đồ thi ta có :

\(\left(d_1\right)\cap\left(d_2\right)=A\left(2;4\right)\)

3) \(\left(d_2\right)\cap Ox=B\left(a;0\right)\)

\(\Leftrightarrow-\dfrac{1}{2}a+5=0\)

\(\Leftrightarrow\dfrac{1}{2}a=5\)

\(\Leftrightarrow a=10\)

\(\Rightarrow\left(d_2\right)\cap Ox=B\left(10;0\right)\)

4) \(OA=\sqrt[]{\left(2-0\right)^2+\left(4-0\right)^2}=\sqrt[]{20}=2\sqrt[]{5}\)

   \(OB=\sqrt[]{\left(10-0\right)^2+\left(0-0\right)^2}=\sqrt[]{10^2}=10\)

  \(AB=\sqrt[]{\left(10-2\right)^2+\left(0-4\right)^2}=\sqrt[]{80}=4\sqrt[]{5}\)

Ta thấy :

 \(OA^2+AB^2=20+80=OB^2=100\)

\(\Rightarrow\Delta OAB\) vuông tại A

\(\Rightarrow\widehat{OAB}=90^o\)

\(sin\widehat{AOB}=\dfrac{AB}{OB}=\dfrac{4\sqrt[]{5}}{10}=\dfrac{2\sqrt[]{5}}{5}\)

\(\Rightarrow\widehat{AOB}\sim63,43^o\)

\(\Rightarrow\widehat{OBA}=90^o-63,43^o=26,57^o\)

5) Chu vi \(\Delta OAB\) :

\(AB+OA+OB=4\sqrt[]{5}+2\sqrt[]{5}+10=10\sqrt[]{5}+10=10\left(\sqrt[]{5}+1\right)\left(đvmd\right)\)

Diện tích \(\Delta OAB\) :

\(\dfrac{1}{2}AB.OA=\dfrac{1}{2}.4\sqrt[]{5}.2\sqrt[]{5}=20\left(đvdt\right)\)

a: 

b: Phương trình hoành độ giao điểm là:

\(2x+7=-\dfrac{1}{2}x+2\)

=>\(2x+\dfrac{1}{2}x=2-7=-5\)

=>2,5x=-5

=>x=-2

Thay x=-2 vào y=2x+7, ta được:

\(y=2\cdot\left(-2\right)+7=7-4=3\)

Vậy: A(-2;3)

c: Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\2x+7=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x=-3,5\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=4\end{matrix}\right.\)

Vậy: C(4;0)

A(-2;3); B(-3,5;0); C(4;0)

\(AB=\sqrt{\left(-3,5+2\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\)

\(AC=\sqrt{\left(4+2\right)^2+\left(0-3\right)^2}=3\sqrt{5}\)

\(BC=\sqrt{\left(4+3,5\right)^2+\left(0-0\right)^2}=7,5\)

Vì \(AB^2+AC^2=BC^2\)

nên ΔABC vuông tại A

=>\(\widehat{BAC}=90^0\)

Xét ΔABC vuông tại A có \(sinABC=\dfrac{AC}{BC}=\dfrac{3\sqrt{5}}{7,5}\)

=>\(\widehat{ABC}\simeq63^0\)

ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=90^0-63^0=27^0\)

d: Chu vi tam giác ABC là:

\(C_{ABC}=AB+AC+BC=\dfrac{3\sqrt{5}}{2}+3\sqrt{5}+7,5=\dfrac{9\sqrt{5}+15}{2}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot\dfrac{3\sqrt{5}}{2}\cdot3\sqrt{5}=\dfrac{45}{4}\)

a) dễ

b)phương trình hoành độ  giao điểm

a) tự vẽ

b) pt hoành độ

x^2=x+2

giải ra được x1=...;x2=,,,,,

thay x1=...;x2=... vô y=x^2

ta được y1=...;y2=...

ta được A;B có vị trí A(x1;y1);B(x2;y2)

Tìm tọa độ trung điểm của AB là C (a;b) ạ 

a, bạn tự vẽ 

b, Hoành độ giao điểm tm pt 

\(\dfrac{x^2}{2}=\dfrac{x}{2}+3\Leftrightarrow x^2-x-6=0\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\Leftrightarrow x=3;x=-2\)

hay \(x_A=3;x_B=-2\)

\(\Rightarrow y_A=\dfrac{9}{2};y_B=2\)

Vậy (P) cắt (d) tại A(3;9/2) ; B(-2;2) 

c, Ta có \(AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\dfrac{5\sqrt{5}}{2}\)

Theo Pytago ta có \(OA=\sqrt{\left(\dfrac{9}{2}\right)^2+3^2}=\dfrac{3\sqrt{13}}{2}\)

Theo Pytago ta có \(OB=\sqrt{2^2+2^2}=2\sqrt{2}\)

Chu vi tam giác ABC là 

\(AB+OA+OB=\dfrac{5\sqrt{5}+3\sqrt{13}+4\sqrt{2}}{2}\)