a: 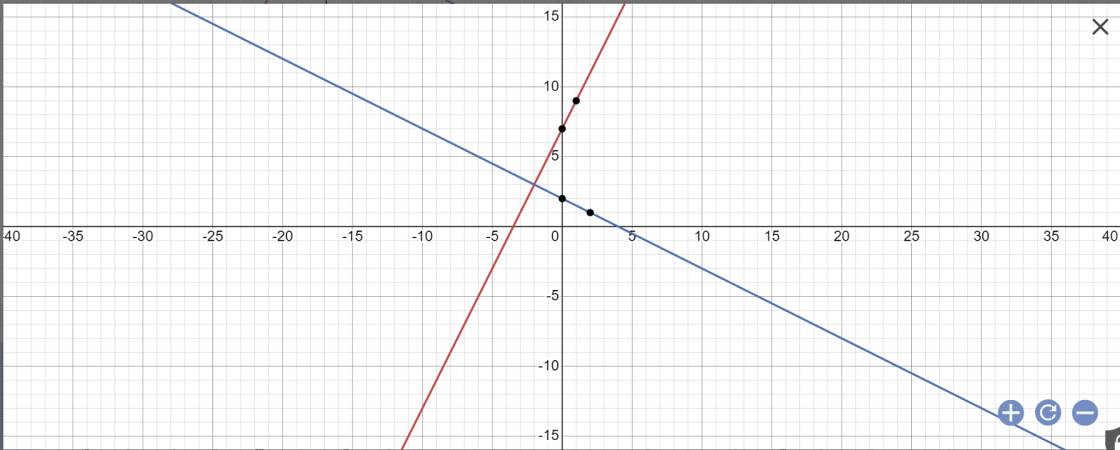
b: Phương trình hoành độ giao điểm là:
\(2x+7=-\dfrac{1}{2}x+2\)
=>\(2x+\dfrac{1}{2}x=2-7=-5\)
=>2,5x=-5
=>x=-2
Thay x=-2 vào y=2x+7, ta được:
\(y=2\cdot\left(-2\right)+7=7-4=3\)
Vậy: A(-2;3)
c: Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x+7=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=-3,5\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=4\end{matrix}\right.\)
Vậy: C(4;0)
A(-2;3); B(-3,5;0); C(4;0)
\(AB=\sqrt{\left(-3,5+2\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\)
\(AC=\sqrt{\left(4+2\right)^2+\left(0-3\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+3,5\right)^2+\left(0-0\right)^2}=7,5\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
Xét ΔABC vuông tại A có \(sinABC=\dfrac{AC}{BC}=\dfrac{3\sqrt{5}}{7,5}\)
=>\(\widehat{ABC}\simeq63^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-63^0=27^0\)
d: Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=\dfrac{3\sqrt{5}}{2}+3\sqrt{5}+7,5=\dfrac{9\sqrt{5}+15}{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot\dfrac{3\sqrt{5}}{2}\cdot3\sqrt{5}=\dfrac{45}{4}\)












