3.22x+1+1/2=49/2

Những câu hỏi liên quan
Biết rằng phương trình 23x - 3.22x+1 + 11.2x – 6 0 có ba nghiệm phân biệt
x
1
,
x
2
,
x
3
.Tính S x1 + x2 + x3 A. log224 B. log212 C. log218 D. log26
Đọc tiếp
Biết rằng phương trình 23x - 3.22x+1 + 11.2x – 6 = 0 có ba nghiệm phân biệt x 1 , x 2 , x 3 .Tính S = x1 + x2 + x3
A. log224
B. log212
C. log218
D. log26
Chọn D.
Phương trình ![]()
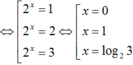 thỏa mãn (*)
thỏa mãn (*)
Do đó S = 1+ log23 = log26.
Đúng 0
Bình luận (0)
Phương trình
3.2
2
x
+
6
−
2
x
3
−
x
−
3
x
−
10
.2
x
có tổng các nghiệm là A.
1...
Đọc tiếp
Phương trình 3.2 2 x + 6 − 2 x = 3 − x − 3 x − 10 .2 x có tổng các nghiệm là
A. 1 − log 2 1 3 .
B. 1 + log 2 3.
C. log 2 1 3 .
D. log 2 2 3 .
Đáp án D
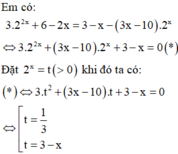
Coi là phương trình bậc hai ẩn t, tính ∆ theo biến em có:
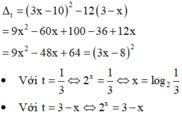
Xét hàm số f x = 2 x đồng biến trên − ∞ ; + ∞ , hàm số g x = 3 − x nghịch biến trên − ∞ ; + ∞
Mà f(1) = g(1) => Phương trình có nghiệm duy nhất x = 1
Vậy phương trình (*) có 2 nghiệm => tổng các nghiệm là
1 + log 2 1 3 = log 2 2 + log 2 1 3 = log 2 2 3
Đúng 0
Bình luận (0)
\((1/49-1/2^2)*(1/49-1/3^2)*.....*(1/49-1/40^2)\)
cho p=1/2+1/3+1/4+…+1/47+1/48+1/49+1/50
q=1/49+2/48+3/49+…47/3+48/2+49/1
tính p/q
Mọi người giúp mình câu này với!!!!!! Tính A=(1/49-1/2^2)(1/49-1/3^2).....(1/49-1/100^2)
\(A=\left(\dfrac{1}{49}-\dfrac{1}{2^2}\right)\left(\dfrac{1}{49}-\dfrac{1}{3^2}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{100^2}\right)\)
\(=\left(\dfrac{1}{49}-\dfrac{1}{7^2}\right)\left(\dfrac{1}{49}-\dfrac{1}{2^2}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{100^2}\right)\)
\(=\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\left(\dfrac{1}{49}-\dfrac{1}{4}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{10000}\right)\)
=0
Đúng 1
Bình luận (0)
Tính S/P biết:
S = 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/49 + 1/50
P = 1/49 + 2/48 + 3/47 + ... + 48/2 +49/1
So sánh tổng : S = 1/5 + 1/9 + 1/10 + 1/41 + 1/42 với 1/2
Đúng 1
Bình luận (0)
S=
=50/50+50/49+50/48+...+50/2
=50.(1/50+1/49+1/48+...+1/4+1/3+1/2)
=50
P=
P=(1/49+1)+(2/48+1)+...+(48/2+1)+1
P= 50/49+50/48+....+50/2+50/50=1
vậy s/p = 1/50
Đúng 6
Bình luận (0)
Cho
A=1/2+1/3+...+1/49+1/50
B=1/49+2/48+...+48/2+49/2
Cho S=1/2+1/3+1/4+....+1/48+1/49+1/5000 và P=1/49+2/48+3/47+....+48/2+49/2.Hãy tính S/P
S=1/2+1/3+1/4+....+1/49+1/50,P=1/49+2/48+3/47+....+48/2+49/1,hay tim S/P
P = 1/49+2/48+3/47+...+48/2+49/1
Cộng 1 váo mỗi p/s trong 48 p/s đầu , trừ p/s cuối đi 48 ta đượ
P=(1/49+1)+(2/48+1)+...+(48/2+1)+1
P= 50/49+50/48+....+50/2+50/50
Đưa ps cuối lên đầu
P=50/50+50/49+50/48+...+50/2
=50.(1/50+1/49+1/48+...+1/4+1/3+1/2)
=50.S
VậyS/P=1/50
Đúng 5
Bình luận (0)
Xem thêm câu trả lời
Tính
\(\left(\frac{1}{49}-\frac{1}{3^2}\right)\left(\frac{1}{49}-\frac{1}{4^2}\right)...\left(\frac{1}{49}-\frac{1}{49^2}\right)\)






















