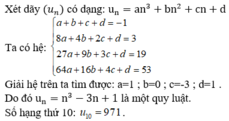tìm quy luật của dãy số 2,3,7,16,32,57,93,142...

Những câu hỏi liên quan
Cho dãy số có quy luật như sau: 2,3,7,16,32,57,93,142...
Hãy tính tổng số hạng thứ 24 và số hạng 40 và tìm quy luật
Sửa lại:
Số hạng thứ 24: 4902
Số hạng thứ 40: 22142
-Quy luật:
Một số hạng ở vị trí n bằng tổng của n2 và số hạng ở vị trí n-1.
\(\left(a_n=n^2+a_{n-1}\right)\) (với n∈N*)
Hoặc \(a_n=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+2\)
Đúng 1
Bình luận (0)
Số hạng thứ 24: 4907.
Số hạng thứ 40: 23736.
-Quy luật: Một số hạng ở vị trí n bằng tổng của n2 và số hạng ở vị trí n-1.
\(\left(a_n=n^2+a_{n-1}\right)\)
Đúng 0
Bình luận (0)
Cho dãy số có 4 số hạng đầu là: -1,3,19,53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm. A.
u
10
97
B.
u
10
71
C.
u
10
1414
D.
u
10
971
Đọc tiếp
Cho dãy số có 4 số hạng đầu là: -1,3,19,53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.
A. u 10 = 97
B. u 10 = 71
C. u 10 = 1414
D. u 10 = 971
Cho dãy số có 4 số hạng đầu là: -1, 3, 19, 53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.
Cho dãy số viết theo quy luật: -1; -2; -1/2; -3; -1 và 1/2; -2/3; -1/4; -5;...
a) Tìm quy luật của dãy số.
b) Số hạng thứ 124 của dãy là số nào?
Cho dãy số 1;5;9;13;...Tìm quy luật của dãy số.
Ta thấy: 5-1=4; 9-5=4; 13-9=4; ....
Vậy quy luật của dãy số là: Hai số liên tiếp nhau hơn kém nhau 4 đơn vị.
Đúng 0
Bình luận (0)
nguyễn trung hiếu phải là các số tự nhiên liên tiếp chia 4 dư 1 chứ không phải số tự nhiên chia 4 dư 1
Đúng 0
Bình luận (0)
Cho dãy số: 2,6,12,20.
Tìm ba số hạng tiếp theo của dãy số
Và tìm quy luật
Đọc tiếp
Cho dãy số: 2,6,12,20.
Tìm ba số hạng tiếp theo của dãy số
Và tìm quy luật
Số thứ n được tính bằng: \(n\left(n+1\right)\)
3 số tiếp theo là:
\(5\left(5+1\right)=30\)
\(6\left(6+1\right)=42\)
\(7\left(7+1\right)=56\)
Đúng 0
Bình luận (0)
Cho dãy số viết theo quy luật
-1;-2;-1/2;-3;-1;-1/3;-4;-3/2;-4;-3/2;-2/3;-1/4;-5.
A. Tìm quy luật của dãy số
B. Tìm số hạng thứ 124 của dãy số
Cho dãy số 1,4,7,10,... Hãy tìm quy luật của dãy số và tìm số thứ 10,thứ 100 của dãy số đó
Quy luật:Số sau hơn số trước 3 đơn vị
Số thứ 10 là:
(10-1)x3+1=28
Số thứ 100 là:
(100-1)x3+1=298
Đúng 0
Bình luận (0)
Cho biết dãy số left( {{a_n}} right) được xác định theo một quy luật nào đó và bốn số hạng đầu tiên của nó được cho như ở bảng dưới đây:a) Tìm quy luật của dãy số và tìm ba số hạng tiếp theo của nó.b) Nếu viết các số hạng của dãy số dưới dạng luỹ thừa, thì bốn số hạng đầu tiên có thể viết thành {2^4};{2^3};{2^2};{2^1}. Dự đoán cách viết dưới dạng luỹ thừa của ba số hạng tiếp theo của dãy số và giải thích.
Đọc tiếp
Cho biết dãy số \(\left( {{a_n}} \right)\) được xác định theo một quy luật nào đó và bốn số hạng đầu tiên của nó được cho như ở bảng dưới đây:
a) Tìm quy luật của dãy số và tìm ba số hạng tiếp theo của nó.
b) Nếu viết các số hạng của dãy số dưới dạng luỹ thừa, thì bốn số hạng đầu tiên có thể viết thành \({2^4};{2^3};{2^2};{2^1}\). Dự đoán cách viết dưới dạng luỹ thừa của ba số hạng tiếp theo của dãy số và giải thích.
a, Quy luật: Mỗi số hạng kể từ số thứ hai bằng số hạng đứng trước nó chia cho 2.
Vậy ba số hạng tiếp theo là: \(a_5=1;a_6=\dfrac{1}{2};a_7=\dfrac{1}{4}\)
b, Các số hạng của dãy số có dạng \(2^n\) với số mũ của số liền sau ít hơn số mũ của số liền trước 1 đơn vị.
Vậy ta có thể viết ba số hạng tiếp theo là: \(a_5=a^0;a_6=a^{-1};a_7=a^{-2}\)
Đúng 0
Bình luận (0)