Tìm phân số a/b thỏa mãn các điều kiện:4/9<a/b<10/21 và 5a-2b=3
ai giúp mk với
Tìm phân số a/b thỏa mãn các điều kiện:4/9<a/b<10/21 và 5a-2b=3
tìm các số tự nhiên a và b thỏa mãn điều kiện 11/17<a/b<23/29 và 8b-9a=31
Giải cách lớp 6 hộ mik nhé
Tìm GTLN của
\(P=\dfrac{a}{\sqrt{1+2bc}}+\dfrac{b}{\sqrt{1+2ca}}+\dfrac{c}{\sqrt{1+2ab}}\)
với a,b,c là các số lớn hơn 0 thỏa mãn điều kiện : \(a^2+b^2+c^2=1\)
P=\(\dfrac{\sqrt{2}.a}{\sqrt{\left(a^2+\left(b+c\right)^2\right)\left(1+1\right)}}+\dfrac{\sqrt{2}.b}{\sqrt{\left(b^2+\left(a+c\right)^2\right)\left(1+1\right)}}+\dfrac{\sqrt{2}.c}{\sqrt{\left(c^2+\left(b+a\right)^2\right)\left(1+1\right)}}\)>=\(\dfrac{\sqrt{2}.a}{\sqrt{\left(a+b+c\right)^2}}+\dfrac{\sqrt{2}.b}{\sqrt{\left(a+b+c\right)^2}}+\dfrac{\sqrt{2}.c}{\sqrt{\left(a+b+c\right)^2}}\)>=\(\sqrt{2}\)
nhầm dấu tí là dấu lớn hơn bằng còn cách lm thì đúng nhé
Tìm tất cả các bộ 3 số tự nhiên (a,b,c) đồng thời thỏa mãn ba điều kiện sau:
a< b< c
6 < a < 10
8< c< 11
Các số tự nhiên a,b,c thỏa mãn ba điều kiện trên là :
Nếu a = 7 thì b = 8 ; c = 9
Còn nếu a = 8 thì b = 9 ; c = 10
CHÚC BẠN HỌC TỐT TRONG NĂM HỌC 2017-2018
THÂN
Các số tự nhiên a,b,c thỏa mãn ba điều kiện trên là :
\(\orbr{\begin{cases}a=7;b=8;c=9\\a=8;b=9;c=10\end{cases}}\)
TK NHA
cho biểu thức A = ba phần n với n là số nguyên
a) Số nguyên n phải thỏa mãn điều kiện j để A là phân số
b) Tìm phân số A biết n=0 n=2 n= -7
Em điều chỉnh nhé, chưa có biểu thức A đâu!
a)A là phân số <=>\(n\ne0\)
b) với n\(\ne\)0
Ta có : n=0 (Không tm)
n=2 và n=-7(TM)
Thay n=2 vào A ta được \(\dfrac{3}{2}\)
Thay n=-7 Vào A ta được \(\dfrac{-3}{7}\)
a. Số nguyên n khác 0 thì A là phân số.
b. - Thay n = 0 vào A, ta được: \(\dfrac{3}{0}\left(vô.lí\right)\) (A không có giá trị)
- Thay n = 2 vào A, ta được: \(\dfrac{3}{2}\) \(\left(A=\dfrac{3}{2}\right)\)
- Thay n = -7 vào A, ta được: \(\dfrac{3}{-7}\) \(\left(A=\dfrac{3}{-7}\right)\)
Tìm 2 số tự nhiên a;b thỏa mãn điều kiện a+2b=48 và (a;b)+3[a;b]=114
Trong số các số phức z thỏa mãn điều kiện z - 4 + 3 i = 3 gọi z 0 là số phức có mô đun lớn nhất. Khi đó z 0 là:
A. 3
B. 4
C. 5
D. 8
Đáp án D
Cách giải: gọi z=x+yi
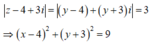
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt 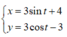
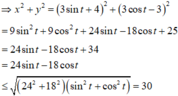
(theo bunhiacopxki)
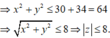
Trong số các số phức z thỏa mãn điều kiện |z-4+3i|=3, gọi z 0 là số phức có mô đun lớn nhất. Khi đó | z 0 | là:
A. 3
B. 4
C. 5
D. 8
Trong các số phức thỏa mãn điều kiện z - 4 i - 2 = 2 i - z , môđun nhỏ nhất của số phức z bằng:
A. 2
B. 3
C. 2 2
D. 2 3
Chứng minh rằng nếu các số tự nhiên a,b,c thỏa mãn điều kiện a^2 + b^2= c^2 thì abc chia hết cho 60
+ Nếu \(a\)\(;\)\(b\) không chia hết cho 3 \(\Rightarrow\) \(a^2;\)\(b^2\)chia 3 dư 1
khi đó \(a^2+b^2\) chia 3 dư 2 \(\Rightarrow\)\(c^2\) chia 3 dư 2 (vô lý)
\(\Rightarrow\)trường hợp \(a\)và \(b\) không chia hết cho 3 không xảy ra \(\Rightarrow\) \(abc\)\(⋮\)\(3\) \(\left(1\right)\)
+ Nếu \(a\)\(;\)\(b\) không chia hết cho 5 \(\Rightarrow\)\(a^2\) chia 5 dư 1 hoặc 4 cà \(b^2\) chia 5 dư 1 hoặc 4
Nếu \(a^2\) chia 5 dư 1 và \(b^2\) chia 5 dư 1 \(\Rightarrow\) \(c^2\) chia 5 dư 2 (vô lí) Nếu \(a^2\) chia 5 dư 1 và \(b^2\) chia 5 dư 4 \(\Rightarrow\) \(c^2\) chia 5 dư 0 \(\Rightarrow\) \(c\)\(⋮\)\(5\) Nếu \(a^2\) chia 5 dư 4 và \(b^2\) chia 5 dư 1 \(\Rightarrow\) \(c^2\) chia 5 dư 0 \(\Rightarrow\) \(c\) \(⋮\)\(5\)Nếu \(a^2\) chia 5 dư 4 và \(b^2\) chia 5 dư 4 \(\Rightarrow\) \(c^2\) chia 5 dư 3 (vô lí). Vậy ta luôn tìm được một giá trị của \(a,\)\(b,\)\(c\)thỏa mãn \(abc\)\(⋮\)\(5\) \(\left(2\right)\)+ Nếu \(a,\)\(b,\)\(c\) không chia hết cho 4 \(\Rightarrow\) \(a^2,\)\(b^2,\)\(c^2\) chia 8 dư 1 hoặc 4
khi đó \(a^2+b^2\) chia 8 dư \(0,\)\(2\)hoặc
\(\Rightarrow\) c2:5 dư 1,4. vô lý => a hoặc b hoặc c chia hết cho 4 (3)
Từ (1) (2) và (3) => abc chia hết cho 60