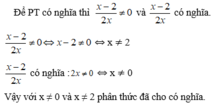Trong điều kiện có nghĩa của biểu thức, chứng minh: \(\frac{cot^22x-1}{2cot2x}-cos8x.cot4x=sin8x\)
Những câu hỏi liên quan
A=cos8x.cot4x-\(\frac{\left(cot^22x-1\right)}{2cot2x}\)
B=cos10x -2cos24x+6cos3x.cosx-cosx -8cosx.cos33x
Trong điều kiện có nghĩa của biểu thức, hãy chứng minh:
\(\frac{1-cosx}{sinx}\left[\frac{\left(1+cosx\right)^2}{sinx^2}-1\right]=2cotx\)
\(VT=\frac{1-cosx}{sinx}\left[\frac{\left(1+cosx\right)^2}{sin^2x}-1\right]\)
\(=\frac{1-cosx}{sinx}.\left[\frac{2\left(1+cosx\right)-sin^2x}{sin^2x}-1\right]\)
\(=\frac{2\left(1-cos^2x\right)}{sin^3x}-\frac{2\left(1-cosx\right)}{sinx}\)
\(=\frac{2}{sinx}-\frac{2-2cosx}{sinx}\)
\(=\frac{2cosx}{sinx}=2cotx\)
Đúng 0
Bình luận (0)
Câu 1 : chứng minh rằng : cot x-tanx = 2cot2x
Câu 2 : chứng minh rằng : \(\frac{cos^2x-sin^2x}{1+sin2x}=\frac{1-tanx}{1+tanx}\)
\(cotx-tanx=\frac{cosx}{sinx}-\frac{sinx}{cosx}=\frac{cos^2x-sin^2x}{sinx.cosx}=\frac{cos2x}{\frac{1}{2}sin2x}=2cot2x\)
\(\frac{cos^2x-sin^2x}{1+sin2x}=\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{sin^2x+cos^2x+2sinx.cosx}=\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{\left(cosx+sinx\right)^2}=\frac{cosx-sinx}{cosx+sinx}\)
\(=\frac{\frac{cosx}{cosx}-\frac{sinx}{cosx}}{\frac{cosx}{cosx}+\frac{sinx}{cosx}}=\frac{1-tanx}{1+tanx}\)
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến để các phân thức sau có nghĩa - 5 x + 2 3 x + 2 2 x - 1 - 1
Để phân thức xác định ta có: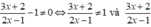 
có nghĩa:
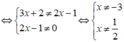
Vậy với x ≠ -3 và x ≠ ½ thì phân thức đã cho được xác định
Đúng 0
Bình luận (0)
Chứng minh
a) \(\frac{sin^22x+4sin^2x-4}{1-8sin^2x-cos4x}=\frac{1}{2}cot^4x\)
b) \(\frac{cos2x}{cot^2x-tan^2x}=\frac{1}{4}sin^22x\)
\(\frac{sin^22x+4sin^2x-4}{1-8sin^2x-cos4x}=\frac{4sin^2x.cos^2x-4\left(1-sin^2x\right)}{1-8sin^2x-\left(1-2sin^22x\right)}=\frac{4sin^2x.cos^2x-4cos^2x}{2sin^22x-8sin^2x}\)
\(=\frac{-4cos^2x\left(1-sin^2x\right)}{8sin^2x.cos^2x-8sin^2x}=\frac{-4cos^2x.cos^2x}{-8sin^2x\left(1-cos^2x\right)}=\frac{cos^4x}{2sin^4x}=\frac{1}{2}cot^4x\)
\(\frac{cos2x}{cot^2x-tan^2x}=\frac{cos2x.sin^2x.cos^2x}{cos^4x-sin^4x}=\frac{\left(cos^2x-sin^2x\right).\left(2sinx.cosx\right)^2}{4\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)}=\frac{1}{4}sin^22x\)
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến để các phân thức sau có nghĩa 3 x - 5 x - 2 2 x
Cho biểu thức: \(A=\left(\frac{x}{x+1}+\frac{1}{1-x}\right):\left(\frac{2x+2}{x-1}-\frac{4x}{x^2-1}\right)\)
a) Tìm điều kiện của x để giá trị của biểu thức được xác định.
b) Chứng minh rằng với điều kiện đó, giá trị của biểu thức không phụ thuộc vào biến.
Với giả thiết biểu thức có nghĩa hãy rút gọn: \(A=\frac{\cos7x-\cos8x-\cos9x+\cos10x}{\sin7x-\sin8x-\sin9x+\sin10x}\)
\(A=\frac{cos7x-cos8x-cos9x+cos10x}{sin7x-sin8x-sin9x+sin10x}=\frac{(cos10x+cos7x)-\left(cos9x+cos8x\right)}{\left(sin10x+sin7x\right)-\left(sin9x+sin8x\right)}.\)
\(=\frac{2cos\frac{17x}{2}cos\frac{3x}{2}-2cos\frac{17x}{2}cos\frac{x}{2}}{2sin\frac{17x}{2}cos\frac{3x}{2}-2sin\frac{17x}{2}cos\frac{x}{2}}=\frac{2cos\frac{17x}{2}\left(cos\frac{3x}{2}-cos\frac{x}{2}\right)}{2sin\frac{17x}{2}\left(cos\frac{3x}{2}-cos\frac{x}{2}\right)}=cotan\frac{17x}{2}.\)
Đúng 0
Bình luận (0)
Cho biểu thức \(A=\frac{3x+2}{2x-2}+\frac{4x}{x^2-1}.\frac{x+1}{8}\)
Tìm điều kiện của x để biểu thức A có nghĩa.