Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A(2;-3), B(3;-2)
a) Viết phương trình đường trung trực của AB
b) Biết tam giác có diện tích bằng \(\frac{9}{2}\) và đỉnh C thuộc đường thẳng \(d:3x-y-8=0\). Tìm tọa độ đỉnh C
Những câu hỏi liên quan
15 tháng 2 2023 lúc 20:01
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1), B(4;5) và C(-3;2). Lập phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x + 3y - 11 = 0
B. -3x + 7y + 13 = 0
C. 3x + 7y + 1 = 0
D. 7x + 3y + 13 = 0
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)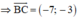 
Phương trình đường cao AH đi qua A(2;-1) nhận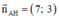 
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)
Mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có A(2;4); B(5;1); C(-1;-2) Phép tịnh tiến T B C → biến tam giác ABC thành tam giác A’B’C’. Tọa độ trọng tâm của tam giác A’B’C’ là
A. (-4;2)
B. (4;2)
C. (4;-2)
D. (-4;-2)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm
G
(
2
3
;
0
)
, biết
M
(
1
;
1
)
là trung điểm cạnh BC. Tọa độ đỉnh A là: A. (2;0) B. (-2;0) C. (0;-2) D. (0;2)
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ( 2 3 ; 0 ) , biết M ( 1 ; 1 ) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A. (2;0)
B. (-2;0)
C. (0;-2)
D. (0;2)
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC với A(1;0;0), B(3;2;4), C(0;5;4). Tìm tọa độ điểm M thuộc mặt phẳng Oxy sao cho
M
A
→
+
M
B
→
+
2
M
C
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC với A(1;0;0), B(3;2;4), C(0;5;4). Tìm tọa độ điểm M thuộc mặt phẳng Oxy sao cho M A → + M B → + 2 M C → nhỏ nhất.
A. M(1;-3;0)
B. M(1;3;0)
C. M(3;1;0)
D. M(2;6;0)
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r= 2√10 -5. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r=2√10-5
. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.
Câu 4.(2 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A 1;3 , B 2;1,C0;3 a). Tìm tọa độ trọng tâm tam giác ABC. b). Viết phương trình tổng quát đường trung trực của tam giác ABC. c). Tính khoảng cách từ A đến đường thẳng : x − y + 1 = 0
a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ
O
x
y
z
, cho tam giác ABC có đỉnh
C
-
2
;
2
;
2
và trọng tâm
G
-
1
;
2
;
2
.
Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt...
Đọc tiếp
Trong không gian với hệ tọa độ O x y z , cho tam giác ABC có đỉnh C - 2 ; 2 ; 2 và trọng tâm G - 1 ; 2 ; 2 . Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt phẳng (Oxy) và điểm B thuộc trục cao.
A. A(-1;-1;0), B(0;0;4)
B. A(-1;1;0), B(0;0;4)
C. A(-1;0;1), B(0;0;4)
D. A(-4;4;0), B(0;0;1)
