cho tam giác abc có a(2 3) b(-1 4) c(3,0) tính diện tích tam giác abc

Những câu hỏi liên quan
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE1/3 BEa) so sánh diện tích tam giác abe với diện tích tam giác abcb) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2c) tính diện tích tứ giác abcedCho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE1/3 BEa) so sánh diện tích tam giác abe với diện tích tam giác abcb) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2c) tính diện tích tứ giác abcedCho tam...
Đọc tiếp
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE=1/3 BE
a) so sánh diện tích tam giác abe với diện tích tam giác abc
b) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2
c) tính diện tích tứ giác abced
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE=1/3 BE
a) so sánh diện tích tam giác abe với diện tích tam giác abc
b) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2
c) tính diện tích tứ giác abced
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE=1/3 BE
a) so sánh diện tích tam giác abe với diện tích tam giác abc
b) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2
c) tính diện tích tứ giác abced
xin lỗi mọi người là tính tứ giác aced chứ ko phải acbed
Đúng 0
Bình luận (0)
Giải:
a) Diện tích tam giác ABC = 1/2 x AH x BC
Diện tích tam giác ABE = 1/2 x AH x BE
= 1/2 x AH x 2/3 BC
= 1/2 x AH x BC x 2/3
= Diện tích tam giác ABC x 2/3
Vậy: Diện tích tam giác ABE = 2/3 diện tích tam giác ABC.
b) Vì chiều cao DE có D là trung điểm nên Diện tích tam giác ABE = 2 lần diện tích tam giác BDE
= 12 x 2
= 24
Diện tích tam giác ABC = 24 : 2/3
= 36
c) Diện tích hình tứ giác ADEC là: 36 - 24 = 12 ( cm vuông)
Đáp số: ...........................
Đúng 0
Bình luận (0)
Giải
Chiều cao là:
15 x 2/6=6 (cm)
Diện tích tam giác ABC là:
7 x 6/2 =21 (cm2
)
Đáp số
Xem thêm câu trả lời
Bài 1: Cho tam giác ABC có AB 2cm, BC 4 cm, CA 3 cm
Tính overrightarrow{AB}.overrightarrow{AC}
Bài 2: Cho tam giác ABC có A ( 1; -1), B ( 5,-3), C ( 2,0)
a) Chứng minh rằng : A,B,C là 3 đỉnh của tam giác
Tính chu vi và diện tích của tam giác
b) Tìm tọa độ M biết overrightarrow{CM}2overrightarrow{AB}-3overrightarrow{AC}
c) Tìm tâm bán kính đường tròn ngoại tiếp tam giác ABC
Đọc tiếp
Bài 1: Cho tam giác ABC có AB = 2cm, BC= 4 cm, CA = 3 cm
Tính \(\overrightarrow{AB}.\overrightarrow{AC}\)
Bài 2: Cho tam giác ABC có A ( 1; -1), B ( 5,-3), C ( 2,0)
a) Chứng minh rằng : A,B,C là 3 đỉnh của tam giác
Tính chu vi và diện tích của tam giác
b) Tìm tọa độ M biết \(\overrightarrow{CM}=2\overrightarrow{AB}-3\overrightarrow{AC}\)
c) Tìm tâm bán kính đường tròn ngoại tiếp tam giác ABC
Xho 4 điểm vectow a(2:0:1) b(1:-1:2) c(2:3:1)d(2:-3:2)
Cm tam giác abc có góc a là tù
Tìm chu vi và diện tích tam giác abc
Tìm M thuộc oy sao cho tam giác mbc vuong góc m
Tính thể tích abcd
1) Cho hình tam giác ABC có AD = 1/3 AC, BE = 1/2 BD, diện tích hình tam giác EBC là 1,2 cm2. Tính diện tích hình tam giác ABC.
2)Cho hình tam giác vuông ABC có AB = 3cm, AC = 4cm. Trên các cạnh của hình tam giác ABC có BG = 1/2 BC; BD = 1/3 BA; AE = 1/4 AC. Tính diện tích hình tam giác DEG.
.Bài 1. cho tam giác Abc cân tại A. có AB 5. BC 8. tính diện tích tam giác ABC.Bài 2. cho tam giác ABC, trung tuyến AM. E thuộc AB sao cho AE 1/3 AB. Chứng minh : a)diện tích tam giác AME ½ diện tích tam giác BMEb) diện tích tam giác AME 1/6 diện tích tam giáCABcBài 3. hình thang ABCD có AB // CD. AC giaomBD tại O. chứng minh diện tích tam giác AOD diện tích tam giác BOCBài 4.cho tam giác ABC. D thuộc AB sao cho AD 1/3 AB. E thuộc BC sao cho BE 1/3 BC, F thuộc AC sao cho CF 1/3 CA. Chứn...
Đọc tiếp
.Bài 1. cho tam giác Abc cân tại A. có AB = 5. BC = 8. tính diện tích tam giác ABC.
Bài 2. cho tam giác ABC, trung tuyến AM. E thuộc AB sao cho AE = 1/3 AB. Chứng minh :
a)diện tích tam giác AME = ½ diện tích tam giác BME
b) diện tích tam giác AME = 1/6 diện tích tam giáCABc
Bài 3. hình thang ABCD có AB // CD. AC giaomBD tại O. chứng minh diện tích tam giác AOD = diện tích tam giác BOC
Bài 4.cho tam giác ABC. D thuộc AB sao cho AD = 1/3 AB. E thuộc BC sao cho BE = 1/3 BC, F thuộc AC sao cho CF = 1/3 CA. Chứng minh
a)iện tích tam giác ADM = 1/3 diện tích tam giác ABN ( làm được rồi )
b)iện tích tam giác ABM = ½ diện tích tam giác ACM ( làm đc rồi )
c) diện tích tam giác AMD = 1/21 diện tích tam giác ABC
d) diện tích tam giác MNP = 1/7 diện tích tam giác ABC
.help meeee. toán 8 ạ
Cho tam giác ABC có A(5;3) : B(2;-1) và C(-1; 5). Tính diện tích tam giác ABC.
A. 5
B. 10
C. 15
D. 20
Chọn C.
Gọi A’ là chân đường cao kẻ từ A.
Theo câu 64 ta có tọa độ điểm A’ là A’(1;1)
Ta có
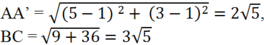
Suy ra ![]()
Đúng 0
Bình luận (0)
Cho tam giác ABC với A(-1; -1), B(2; -4), C(4; 3). Diện tích tam giác ABC là:
A.3/2
B.9/2
C.27/2
D.13
Ta có: B C = ( 4 − 2 ) 2 + ( 3 + 4 ) 2 = 53
Phương trình BC : Qua B (2; -4) và nhận VTCP
B
C
→
(
2
;
7
)
nên có VTPT
n
→
(
7
;
−
2
)
:
7( x -2) – 2 ( y + 4) = 0 hay 7x - 2y - 22 = 0
Khoảng cách từ A đến BC là:
d ( A ; B C ) = 7. ( − 1 ) − 2. ( − 1 ) − 22 7 2 + ( − 2 ) 2 = 27 53
Diện tích tam giác ABC là: S = 1 2 B C . d ( A ; B C ) = 1 2 . 53 . 27 53 = 27 2
ĐÁP ÁN C.
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(-2;-1).
a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.
b) Tính diện tích tam giác ABC.
a) Ta có: \(\overrightarrow {{u_{BC}}} = \overrightarrow {BC} = \left( { - 5; - 3} \right) \Rightarrow \overrightarrow {{n_{BC}}} = \left( {3; - 5} \right)\) . Vậy phương trình tổng quát của đường thẳng BC là: \(3\left( {x - 3} \right) - 5\left( {y - 2} \right) = 0 \Leftrightarrow 3x - 5y + 1 = 0\).
Độ dài đường cao AK của tam giác \(ABC\) hạ từ đỉnh A là: \(AK = d\left( {A,BC} \right) = \frac{{\left| {3.1 - 0.5 + 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 5} \right)}^2}} }} = \frac{4}{{\sqrt {34} }}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 5; - 3} \right) \Rightarrow BC = \sqrt {{{\left( { - 5} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {34} \)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AK.BC = \frac{1}{2}.\frac{4}{{\sqrt {34} }}.\sqrt {34} = 2\)
Đúng 0
Bình luận (0)
Câu 4 (3 điểm): Cho tam giác ABC có diện tích 64cm2 . Trên cạnh AB lấy điểm M sao cho AM = 1/ 4 AB. Trên cạnh AC lấy điểm N sao cho AN = 1/ 4 AC. Nối B với N. a) Tính diện tích tam giác BNC. b) Tính tỉ số diện tích tam giác AMN và tam giác ABC. c) Qua A vẽ một đường thẳng cắt MN ở K và cắt BC ở E. Tính tỉ số KE /AK .
cho tam giác ABC có BC bằng 8cm, đường cao AH 5cm. MA bằng 1/3 AB, NA bằng 1/4 AC.
a) tính diện tích tam giác ABC
b) tính diện tích tam giác AMN
Nối M với C
a) Diện tích tam giác ABC là :
( 8 x 5 ) : 2 = 20 (cm2)
\(S_{AMC}=\frac{1}{3}S_{ABC}\)(1)
- Chung cao hạ từ C xuống AB
- Đáy AM = 1/3 AB
\(S_{AMN}=\frac{1}{4}S_{AMC}\)(2)
- Đáy AN = 1/4 AC
- Chung cao hạ từ M xuống AC
Từ (1) và (2) suy ra :
\(S_{AMN}=\frac{1}{3}\cdot\frac{1}{4}=\frac{1}{12}S_{ABC}\)
\(S_{AMN}=\frac{20}{12}cm^2\)
Đúng 0
Bình luận (0)
















