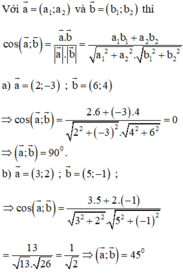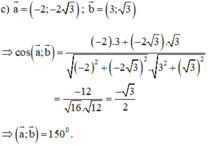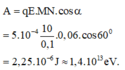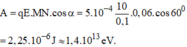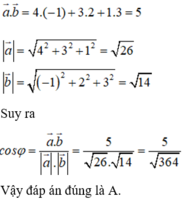tính góc tạo bởi giữa hai vectơ trong trường hợp a(3;4),b(-4;3)

Những câu hỏi liên quan
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ a→ và b→ trong các trường hợp sau:
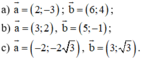
Cho các véctơ
a
→
;
b
→
có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ
u
→
a
→
+
2
b
→
;
v
→
a
→...
Đọc tiếp
Cho các véctơ a → ; b → có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ u → = a → + 2 b → ; v → = a → - b →
A. -1/2
B. -1/4
C. -1/6
D. 0
Chọn C.
Ta có:
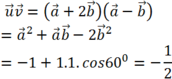
Mặt khác : ![]() nên
nên ![]()
![]() nên
nên ![]()
Suy ra ![]()
Đúng 0
Bình luận (0)
Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)trong các trường hợp sau
a) \(\overrightarrow a = (2; - 3),\overrightarrow b = (6;4)\)
b) \(\overrightarrow a = (3;2),\overrightarrow b = (5; - 1)\)
c) \(\overrightarrow a = ( - 2; - 2\sqrt 3 ),\overrightarrow b = (3;\sqrt 3 )\)
a) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{2.6 + ( - 3).4}}{{\sqrt {{2^2} + {{\left( { - 3} \right)}^2}} .\sqrt {{6^2} + {4^2}} }} = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \)
b) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{3.5 + 2.( - 1)}}{{\sqrt {{3^2} + {2^2}} .\sqrt {{5^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)
c) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{\left( { - 2} \right).3 + ( - 2\sqrt 3 ).\sqrt 3 }}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 2\sqrt 3 } \right)}^2}} .\sqrt {{3^2} + {{\sqrt 3 }^2}} }} = - \frac{{\sqrt 3 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 150^\circ \)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong mỗi trường hợp sau:
a) \(\overrightarrow a = ( - 3;1),\;\overrightarrow b = (2;6)\)
b) \(\overrightarrow a = (3;1),\;\overrightarrow b = (2;4)\)
c) \(\overrightarrow a = ( - \sqrt 2 ;1),\;\overrightarrow b = (2; - \sqrt 2 )\)
a)
\(\overrightarrow a .\overrightarrow b = ( - 3).2 + 1.6 = 0\)
\( \Rightarrow \overrightarrow a \bot \overrightarrow b \) hay \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^o}\).
b)
\(\left\{ \begin{array}{l}\overrightarrow a .\overrightarrow b = 3.2 + 1.4 = 10\\|\overrightarrow a |\, = \sqrt {{3^2} + {1^2}} = \sqrt {10} ;\;\,|\overrightarrow b |\, = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{10}}{{\sqrt {10} .2\sqrt 5 }} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {45^o}\end{array}\)
c) Dễ thấy: \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương do \(\frac{{ - \sqrt 2 }}{2} = \frac{1}{{ - \sqrt 2 }}\)
Hơn nữa: \(\overrightarrow b = \left( {2; - \sqrt 2 } \right) = - \sqrt 2 .\left( { - \sqrt 2 ;1} \right) = - \sqrt 2 .\overrightarrow a \;\); \( - \sqrt 2 < 0\)
Do đó: \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng.
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^o}\)
Chú ý:
Khi tính góc, ta kiểm tra các trường hợp dưới đây trước:
+ \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^o}\): nếu \(\overrightarrow a .\overrightarrow b = 0\)
+ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương:
\(\left( {\overrightarrow a ,\overrightarrow b } \right) = {0^o}\) nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
\(\left( {\overrightarrow a ,\overrightarrow b } \right) = {180^o}\) nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng
Nếu không thuộc các trường hợp trên thì ta tính góc dựa vào công thức \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy Tính tích vô hướng của hai vectơ a và b.
a) biết độ dài vectơ a 8 độ dài vectơ B căn 3 và góc hợp bởi hai vectơ A và vectơ B bằng 30 độ
b) biết độ dài vectơ a căn 2 độ dài vectơ B 6 và góc hợp bởi hai vectơ A và vectơ B bằng 45 độ
c) biết độ dài vectơ a 9 độ dài vectơ B 10 và góc tạo bởi hai vectơ A và B bằng 60 độ
d) biết độ dài vectơ a 5 độ dài vectơ B 6 và góc tạo bởi hai vectơ A và B bằng 120 độ
Đọc tiếp
Trong mặt phẳng Oxy Tính tích vô hướng của hai vectơ a và b.
a) biết độ dài vectơ a = 8 độ dài vectơ B = căn 3 và góc hợp bởi hai vectơ A và vectơ B bằng 30 độ
b) biết độ dài vectơ a = căn 2 độ dài vectơ B = 6 và góc hợp bởi hai vectơ A và vectơ B bằng 45 độ
c) biết độ dài vectơ a = 9 độ dài vectơ B = 10 và góc tạo bởi hai vectơ A và B bằng 60 độ
d) biết độ dài vectơ a = 5 độ dài vectơ B = 6 và góc tạo bởi hai vectơ A và B bằng 120 độ
\(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a};\overrightarrow{b}\right)\)
a/ \(\overrightarrow{a}.\overrightarrow{b}=8.\sqrt{3}.cos30^0=12\)
b/ \(\overrightarrow{a}.\overrightarrow{b}=\sqrt{2}.6.cos45^0=6\)
c/ \(\overrightarrow{a}.\overrightarrow{b}=9.10.cos60^0=45\)
d/ \(\overrightarrow{a}.\overrightarrow{b}=5.6.cos120^0=-15\)
Đúng 0
Bình luận (0)
Một điện tích
q
5.10
−
8
C
di chuyển giữa hai điểm M, N cách nhau 60mm trong điện trường đều của một tụ điện phẳng có hiệu điện thế giữa hai bản tụ là U 150V và khoảng cách giữa hai bản tụ là d 10cm. Góc hợp bởi vecto
M
N
→
và vectơ cường độ điện trường
E
→
là
α...
Đọc tiếp
Một điện tích q = 5.10 − 8 C di chuyển giữa hai điểm M, N cách nhau 60mm trong điện trường đều của một tụ điện phẳng có hiệu điện thế giữa hai bản tụ là U = 150V và khoảng cách giữa hai bản tụ là d = 10cm. Góc hợp bởi vecto M N → và vectơ cường độ điện trường E → là α = 60 0 . Công của lực điện trường làm di chuyển điện tích nhận giá trị nào sau đây?
A. 2 , 4.10 13 e V .
B. 1 , 2.10 − 6 e V .
C. 2 , 25.10 − 6 e V .
D. 1 , 4.10 13 e V .
Một điện tích
q
5
.
10
-
8
C
di chuyển giữa hai điểm M, N cách nhau 60mm trong điện trường đều của một tụ điện phẳng có hiệu điện thế giữa hai bản tụ là U 150V và khoảng cách giữa hai bản tụ là d 10cm. Góc hợp bởi vecto
MN
→
và vectơ cường độ điện trường
E
→
là
α...
Đọc tiếp
Một điện tích q = 5 . 10 - 8 C di chuyển giữa hai điểm M, N cách nhau 60mm trong điện trường đều của một tụ điện phẳng có hiệu điện thế giữa hai bản tụ là U = 150V và khoảng cách giữa hai bản tụ là d = 10cm. Góc hợp bởi vecto MN → và vectơ cường độ điện trường E → là α = 60 o . Công của lực điện trường làm di chuyển điện tích nhận giá trị nào sau đây?
A. 2 , 4 . 10 13 e V
B. 1 , 2 . 10 - 6 e V
C. 2 , 25 . 10 - 6 e V
D. 1 , 4 . 10 13 e V
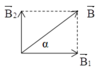
Trong không gian Oxyz, gọi φ là góc tạo bởi hai vectơ
a
→
(4; 3; 1);
b
→
(-1; 2; 3). Trong các khẳng định sau, khẳng định nào đúng? A.
cosφ
5
364
B.
cosφ
5
312
C.
cosφ
5...
Đọc tiếp
Trong không gian Oxyz, gọi φ là góc tạo bởi hai vectơ a → = (4; 3; 1); b → = (-1; 2; 3). Trong các khẳng định sau, khẳng định nào đúng?
A. cosφ = 5 364
B. cosφ = 5 312
C. cosφ = 5 364
D. cosφ = 5 312
Từ trường tại điểm M do dòng điện thứ nhất gây ra có vectơ cảm ứng từ
B
→
1
, do dòng điện thứ hai gây ra có vectơ cảm ứng từ
B
→
2
, hai vectơ
B
→
1
và
B
→...
Đọc tiếp
Từ trường tại điểm M do dòng điện thứ nhất gây ra có vectơ cảm ứng từ B → 1 , do dòng điện thứ hai gây ra có vectơ cảm ứng từ B → 2 , hai vectơ B → 1 và B → 2 có hướng vuông góc với nhau. Góc hợp bởi vectơ cảm ứng từ tổng hợp B → với vectơ B → 1 là α được tinh theo công thức:
A. tanα = B 1 B 2
B. tanα = B 2 B 1
C. sinα = B 1 B
D. cosα = B 2 B