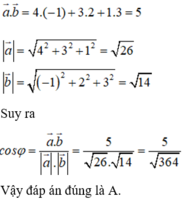Các câu hỏi tương tự
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình
2
x
-
y
+
2
z
+
1
0
, đường thẳng d có phương trình
x
-
1
-
1
y
-
2
x
+
2...
Đọc tiếp
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình 2 x - y + 2 z + 1 = 0 , đường thẳng d có phương trình x - 1 - 1 = y - 2 = x + 2 2 . Gọi φ là góc giữa đường thẳng d và mặt phẳng (P). Tính giá trị cos φ
![]()
![]()
![]()
#2H3Y1-1~Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(2; 1; -1), B(3; 3; 1), C(4; 5; 3). Khẳng định nào đúng? B. A, B, C thẳng hàng C. AB AC D. O, A, B, C là 4 đỉnh của một tứ diện.
Đọc tiếp
#2H3Y1-1~Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(2; 1; -1), B(3; 3; 1), C(4; 5; 3). Khẳng định nào đúng?
![]()
B. A, B, C thẳng hàng
C. AB = AC
D. O, A, B, C là 4 đỉnh của một tứ diện.
Trong không gian Oxyz, cho hai vectơ
a
→
(
x
1
,
y
1
,
z
1
),
b
→
(
x
2
,
y
2
,
z
2
) thay đổi. Trong cá...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ a → = ( x 1 , y 1 , z 1 ), b → = ( x 2 , y 2 , z 2 ) thay đổi. Trong các khẳng định dưới đây, khẳng định nào đúng?
A. a . → b → = a → . b → với mọi a → , b →
B. a . → b → 2 = a → 2 . b → 2 với mọi a → , b →
C. a . → b → < a → . b → với mọi a → , b →
D. a . → b → = 0 ⇔ a → = 0 → hoặc b → = 0 →
Trong không gian Oxyz, cho hai vectơ
a
→
(
x
1
;
y
1
;
z
1
), b→ (
x
2
;
y
2
;
z
2
) thay đổi. Trong các khẳng định dưới đây, khẳng định nào đúng? A. ...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ a → = ( x 1 ; y 1 ; z 1 ), b→ = ( x 2 ; y 2 ; z 2 ) thay đổi. Trong các khẳng định dưới đây, khẳng định nào đúng?
A. a → . b → = x 1 x 2 + y 1 y 2 + z 1 z 2
B. a → . b → > a → . b →
C. a → . b → = a → . b → . sin a → , b →
D. a → = b → ⇔ x 1 2 + y 1 2 + z 1 2 = x 2 2 + y 2 2 + z 2 2
Trong không gian với hệ tọa độ Oxyz, cho các vectơ
a
→
1
;
1
;
0
,
b
→
2
;
-
1
;
-
2
,
c
→
-
3
;
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các vectơ a → = 1 ; 1 ; 0 , b → = 2 ; - 1 ; - 2 , c → = - 3 ; 0 ; 2 . Khẳng định nào đúng?
A. a → b → + c → = 0
B. 2 a → + b → = c →
C. a → = 2 b → - c →
D. a → + b + c → = 0
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
:
x
3
-
t
y
4
+
t
z
5...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : x = 3 - t y = 4 + t z = 5 - 2 t và d ' : x = 2 - 3 t ' y = 5 + 3 t ' z = 3 - 6 t ' Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Trong không gian với hê tọa độ Oxyz, cho hai đường thẳng
d
:
x
1
+
t
y
2
t
z
3
-...
Đọc tiếp
Trong không gian với hê tọa độ Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 t z = 3 - t và d ' : x = 2 + 2 t ' y = 3 + 4 t ' z = 5 - 2 t ' Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho ba vectơ Trong các khẳng định sau, khẳng định nào đúng? A.
a
→
.
b
→
c
→
c
→...
Đọc tiếp
Trong không gian Oxyz, cho ba vectơ ![]()
Trong các khẳng định sau, khẳng định nào đúng?
A. a → . b → c → = c → . b → a → với mọi a → , b → , c →
B. b → + a → c → = a → . c → + b → . c →
C. b → . c → a → ≥ 0
D. a → + b → + c → 2 < 0
Trong không gian Oxyz, cho ba vectơ Trong các khẳng định sau, khẳng định nào đúng? A.
a
→
.
b
→
.
c
→
b
→
.
c
→...
Đọc tiếp
Trong không gian Oxyz, cho ba vectơ ![]()
Trong các khẳng định sau, khẳng định nào đúng?
A. a → . b → . c → = b → . c → . a → với mọi a → , b → , c →
B. a → . b → . c → = b → . c → . a → ⇔ b → = 0 →
C. a → . b → . c → = b → . c → . a → ⇔ a → / / c →
D. a → . b → . c → ≤ a → . b → . c →