A=x2-3x+1 tại x=-1:x=2
a) -(x-y)(x2+xy-1)
b) x2(x-1)-(x2+1)(x-y)
c) (3x-2)(2x-1)+(-5x-1)(3x+2)
d) (3x-5)(2x+11)-(2x3)(3x+7)
Bài 2: Tính giá trị biểu thức
C=x(x2-y)-x2(x+y)+y(x2-x) tại x=1/2, y=-1
a)-(x-y)(x2+xy-1)=-(x3+x2y-x-x2y-xy2+y)
=-(x3-xy2-x+y)
=-x3+xy2+x-y
b)x2(x-1)-(x3+1)(x-y)=x3-x2-x3+x2y-x+y
=-x2+x2y-x+y
c)(3x-2)(2x-1)+(-5x-1)(3x+2)=6x2-3x-4x+2-15x2-10x-3x-2
=-9x2-20x
d) hình như bạn ghi lỗi
Bài 2: C=x(x2-y)-x2(x+y)+y(x2-x)
=x3-xy-x3-x2y+x2y-xy
=-2xy
Thay x=1/2,y=-1 vào C, ta có:
C=-2.1/2.(-1)=1
Vậy C=1 khi x=1/2 và y=-1.
Tính giá trị của phân thức:
a) x 2 − 2 x − 3 x 2 + 2 x + 1 với x ≠ − 1 tại 3 x − 1 = 0 ;
b) x − 2 x 2 − 5 x + 6 với x ≠ 2 ; x ≠ 3 tại x 2 − 4 = 0 .
A(x)= -x3 -x (5x3+2-3x )+2+5x4-12x-x2 tại /x/=1
Ta có: \(A\left(x\right)=-x^3-x\left(5x^3+2-3x\right)+2+5x^4-12x-x^2\)
\(=-x^3-5x^4-2x+3x^2+2+5x^4-12x-x^2\)
\(=-x^3+2x^2-14x+2\)
Thay x=1 vào A(x), ta được:
\(A\left(1\right)=-1^3+2\cdot1^2-14\cdot1+2=-1+2-14+2=1-14+2=3-14=-11\)
Thay x=-1 vào A(x), ta được:
\(A\left(-1\right)=-\left(-1\right)^3+2\cdot\left(-1\right)^2-14\cdot\left(-1\right)+2\)
\(=-\left(-1\right)+2\cdot1+14+2\)
\(=1+2+14+2\)
\(=4+15=19\)
Tính giá trị của phân thức:
a) x 2 − 1 2 x 2 − 3 x + 1 với x ≠ 1 và x ≠ 1 2 tại 2 x + 1 = 3 ;
b) 3 x 2 − 10 x + 3 x 2 − 4 x + 3 với x ≠ 2 ; x ≠ 3 tại x 2 − 8 x + 15 = 0 .
Tính giá trị biểu thức:
a) Q = (3x – 1)(9 x 2 – 3x + 1) – (1 – 3x)(1 + 3x + 9 x 2 ) tại x = 10;
b*) P = x 4 3 + y 2 3 biết xy = 4 và x + 2y = 8.
a) Rút gọn Q = 54 x 3 , thay x = 10 vào tính được Q = 54000;
b) Gợi ý x 4 + y 2 = x + 2 y 4 = 8 4 = 2 . Kết quả P = 2.
rút gọn A,B,C
A=(3x+7)(2x+3)-(3x-5)(2x+11)
B=(x2-2)(x2+x-1)-x(x3+x2-3x-2)
C=x(x3+x2-3x-2)-(x2-2)(x2+x-1)
\(A=6x^2+23x+21-\left(6x^2+23x-55\right)=76\\ B=x^4+x^3-x^2-2x^2-2x+2-x^4-x^3+3x^2+2x\\ =2\\ C=x^4+x^3-3x^2-2x-\left(x^4+x^3-x^2-2x^2-2x+2\right)\\ =-2\)
a. x+1/x-2 - x/x+2 + 8/x2 -4
b. x-3/x+1 - x+2/x-1 + 8x/x2 -1
c. x+2/x2-2x + 2/x2+2x + 3x+2/x2-4
d. 4/x - 12/x2+3x + 5/x+3
a: \(=\dfrac{x^2+3x+2-x^2+2x+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)
b: \(=\dfrac{x^2-4x+3-x^2-3x-2+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)
c: \(=\dfrac{x+2}{x\left(x-2\right)}+\dfrac{2}{x\left(x+2\right)}+\dfrac{3x+2}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+2x+2x-4+3x+2}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+7x-2}{x\left(x-2\right)\left(x+2\right)}\)
a,
\(\dfrac{x+1}{x-2}-\dfrac{x}{x+2}+\dfrac{8}{x^2-4}\\ =\dfrac{x^2+3x+2-x^2+2x+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)
b,
\(\dfrac{x-3}{x+1}-\dfrac{x+2}{x-1}+\dfrac{8x}{x^2-1}\\ =\dfrac{x^2-4x+3-x^2-3x-2+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{1}{x-1}\)
Tìm a để các hàm số f ( x ) 3 x + 1 - 2 x 2 - 1 K h i x > 1 a ( x 2 - 2 ) x - 3 K h i x ≤ 1 liên tục tại x = 1
A. 1/2
B. 1/4
C. 3/4
D. 1
Chọn C.
Ta có : 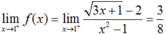
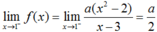
Suy ra hàm số liên tục tại 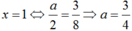
a. x2(x – 2x3) b. (x2 + 1)(5 – x) c. (x – 2)(x2 + 3x – 4) d. (x – 2)(x – x2 + 4) e. (x2 – 1)(x2 + 2x) f. (2x – 1)(3x + 2)(3 – x) g. (x + 3)(x2 + 3x – 5) h. (xy – 2).(x3 – 2x – i. (5x3 – x2 + 2x – 3).(4x2 – x + 2
a: \(=x^3-2x^5\)
e: \(=x^4+2x^3-x^2-2x\)