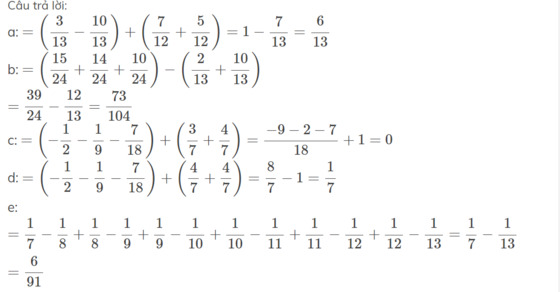m= 1/6 + 1/12 +1/20 + ... + 1/132 + 1/156

Những câu hỏi liên quan
| a) 3/13 + 7/12 - 10/13 + 5/12 | d) -5/10 + 12/28 - 3/27 - 7/18 + 20/35 |
| b) 15/24 - 6/26 + 28/48 - 30/39 + 10/24 | e) 1/56 + 1/72 + 1/90 + 1/110 + 1/132+ 1/156 = |
| c) -1/2 + 3/7 - 1/9 - 7/18 + 4/7 = |
Tính tổng A= 1- 5/6 +7/12 - 9/20 + 11/30 - 13/42 + 15/56 - 17/72 + 19/90 - 21/110 + 23/132 - 25/156
A = 1 - \(\dfrac{5}{6}\)+\(\dfrac{7}{12}\)-\(\dfrac{9}{20}\)+\(\dfrac{11}{30}\)-\(\dfrac{13}{42}\)+\(\dfrac{15}{56}\) - \(\dfrac{17}{72}\)+\(\dfrac{19}{90}\)+\(\dfrac{23}{132}\)-\(\dfrac{25}{156}\)
A = 1 - \(\dfrac{5}{2.3}\)+\(\dfrac{7}{3.4}\)-\(\dfrac{9}{4.5}\)+\(\dfrac{11}{5.6}\)-\(\dfrac{13}{6.7}\)+\(\dfrac{15}{7.8}\)-\(\dfrac{17}{8.9}\)+\(\dfrac{19}{9.10}\)+\(\dfrac{23}{11.12}\)-\(\dfrac{25}{12.13}\)
A = 1 - \(\dfrac{1}{2}-\dfrac{1}{3}\)+\(\dfrac{1}{3}+\dfrac{1}{4}\)-\(\dfrac{1}{4}-\dfrac{1}{5}\)+...+\(\dfrac{1}{11}+\dfrac{1}{12}\)- \(\dfrac{1}{12}-\dfrac{1}{13}\)
A = 1 - \(\dfrac{1}{2}\) - \(\dfrac{1}{13}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{13}\)
A = \(\dfrac{11}{26}\)
Đúng 0
Bình luận (0)
\(S=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{132}+\frac{1}{156}\)
Tính tổng S.
\(S=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{132}+\frac{1}{156}\)
\(S=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{11.12}+\frac{1}{12.13}\)
\(S=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{11}-\frac{1}{12}+\frac{1}{12}-\frac{1}{13}\)
\(S=\frac{1}{1}-\frac{1}{13}\)
\(S=\frac{12}{13}\)
Đúng 0
Bình luận (0)
\(S=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{12.13}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+.....+\frac{1}{12}-\frac{1}{13}\)
\(=1-\frac{1}{13}\)
\(=\frac{12}{13}\)
Đúng 0
Bình luận (0)
1/20+1/30+1/42+1/56+1/72+1/90+1/110+1/132+1/156 = ?
1/20 + 1/30 + 1/42 + ... + 1/156
= 1/4.5 + 1/5.6 + 1/6.7 + .... + 1/12.13
= 1/4 - 1/5 + 1/5 - 1/6 + 1/6 - 1/7 + ... + 1/12 - 1/13
= 1/4 - 1/13
= 9/52
Đúng 0
Bình luận (0)
\(=\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+\frac{1}{8.9}+\frac{1}{9.10}+\frac{1}{10.11}+\frac{1}{11.12}+\frac{1}{12.13}\)
\(=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+....+\frac{1}{12}-\frac{1}{13}\)
\(=\frac{1}{4}-\frac{1}{13}=\frac{9}{52}\)
****
Đúng 0
Bình luận (0)
= 1/4.5 + 1/5.6 + 1/6.7 + 1/7.8 + 1/8.9 + 1/9.10 + 1/10.11 + 1/11.12 + 1/12.13
= 1/4 - 1/5 + 1/5 - 1/6 + ... + 1/2 - 1/13
= 1/4 - 1/13
= 9/52
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính 1/20 + 1/30 + 1/42 + 1/56 + 1/ 72 + 1/90 + 1/110 + 1/ 132 + 1/156
Đặt tổng trên là A ta có :
A= 1/ 20 + 1/ 30 + 1/ 42 + 1/ 56 + 1/ 72 + 1/90 + 1/110 + 1 / 123 + 1/ 156
= 1 / 4 x5 + 1/ 5 x 6 + 1/6x 7 + 1/ 7x8 + 1/8x9 + 1/9x10+ 1/ 10x11+ 1 /11x12 +1/12 x 13
= 1/4- 1/5 + 1/ 5 - 1/6 + 1/ 6 - 1/7 + 1/ 7 - 1/8 + 1/8 - 1/9 + 1/9 - 1/10+ 1/10 - 1/11 + 1/11 - 1/12+ 1/ 12 - 1/13
= 1 /4 - 1 /13
= 9 /52
Đúng 0
Bình luận (0)
A = 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90 + 1/ 110 + 1/132 + 1/156
\(=\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{12.13}\)
áp dụng \(\frac{1}{a.b}=\frac{1}{a}-\frac{1}{b}\)làm sẽ có các số nghịch đảo và được kết quả là 1/4 - 1/13
Đúng 0
Bình luận (0)
A = 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90 + 1/110 + 1/132 + 1/156
A = 1/4.5 + 1/5.6 + 1/6.7 + 1/7.8 + 1/8.9 + 1/9.10 + 1/10.11 + 1/11.12 + 1/12.13
A = 1/4 - 1/5 + 1/5 - 1/6 + 1/6 - 1/7 + 1/7 - 1/8 + 1/8 - 1/9 + 1/9 - 1/10 + 1/10 - 1/11 + 1/11 - 1/12 + 1/12 - 1/13
A = 1/4 - 1/13
A = 9/52
Đúng 0
Bình luận (0)
A = \(\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+...+\frac{1}{132}+\frac{1}{156}\)
= \(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+...+\frac{1}{11.12}+\frac{1}{12.13}\)
= \(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+...+\frac{1}{11}-\frac{1}{12}+\frac{1}{12}-\frac{1}{13}\)
= \(\frac{1}{4}-\frac{1}{13}\)
= \(\frac{9}{52}\)
Vậy \(A=\frac{9}{52}\)
Đúng 0
Bình luận (0)
1/2+1/6+1/12+1/20...+156
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+........+\frac{1}{56}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+...........+\frac{1}{7.8}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+......+\frac{1}{7}-\frac{1}{8}\)
\(=1-\frac{1}{8}=\frac{7}{8}\)
Đúng 0
Bình luận (0)
A=1/2+1/6+1/12+1/20+......+1/132 = ?
1/2 + 1/6 + 1/20 +........+1/110 + 1/132 =
1/2 + 1/2x3 + 1/3x4 + 1/4x5 +....+ 1/10x11 + 1/11x12
= 1/2 + 1/2 - 1/3 + 1/3 -1/4 + 1/4 - 1/5 +...+ 1/10 - 1/11 +1/11 - 1/12
= 1/2 + 1/2 - 1/12 = 1 - 1/12 = 11/12
Đáp số : 11/12
đúng mình cái nha
Đúng 0
Bình luận (0)
tính nhanh:A=1/2+1/6+1/12+1/20+...+1/132
\(A=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{132}\)
\(=\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{11\cdot12}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}=\frac{11}{12}\)
Vậy \(A=\frac{11}{12}\)
Chúc bạn học tốt ^^!!!
\(A=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{132}\)
\(=\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{11\times12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}=\frac{11}{12}\)
Chúc bạn học tốt!
#Huyền#
A=\(\frac{1}{2}\)+\(\frac{1}{6}\)+\(\frac{1}{12}\)+.....+\(\frac{1}{132}\)
A= \(\frac{1}{1x2}\)+\(\frac{1}{2x3}\)+\(\frac{1}{3x4}\)+.....+\(\frac{1}{11x12}\)
A= 1 -\(\frac{1}{2}\)+ \(\frac{1}{2}\)-\(\frac{1}{3}\)+\(\frac{1}{3}\)-\(\frac{1}{4}\)+....+\(\frac{1}{11}\)-\(\frac{1}{12}\)
A= 1-\(\frac{1}{12}\)
A=\(\frac{11}{12}\)
Xem thêm câu trả lời