Cho hình chóp tam giác đều S.ABC. Gọi M là trung điểm BC, G là trọng tâm tam giác ABC, AB = 2a; góc giữa mặt bên và đáy bằng 60.
a/ Tính thể tích chóp S.ABC
b/ Tính khoảng cách giữa SA và BC
Những câu hỏi liên quan
Cho hình chóp S.ABC có đấy ABC là tam giác đều cạnh a, SA = SB = SC = 2a. Gọi o là trung điểm AC, G là trọng tâm tam giác ABC a) chứng minh (SGO) vuông góc với (ABC) b) tính góc giữa hai mặt phẳng (SAB) và (ABC) c) tính khoảng cách giữa AB và SC
a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ
Đúng 0
Bình luận (0)
Cho hình chóp SABC có SA vuông với đáy. SA=2a, tam giác ABC đều có cạnh bằng 4a. Mà M là trung điểm BC
a) CMR: BC vuông với (SAM)
b) Tính d(A;(SBC))
c) Gọi G là trọng tâm tam giác SAB. Tính d(G;(SBC))
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: Kẻ AK vuông góc SM
=>AK=d(A;(SBC))
AM=4a*căn 3/2=2a*căn 3
=>SM=4a
=>AK=2a*2a*căn 3/4a=a*căn 3
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC. Gọi M, N lần lượt là trung điểm của AC, BC và G là trọng tâm tam giác (ABD).
a) Tìm giao tuyến giữa PN và (BDI) với I là trung điểm của NC.
b) TÌm thiết diện hình chóp cắt bởi (CMP)
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC).
b) Tính khoảng cách giữa hai đường thẳng AB và SG.
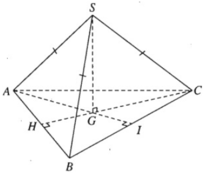
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
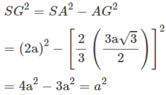
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
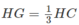
mà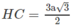 
nên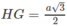 
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC, điểm G là trọng tâm của tam giác SBC. Gọi K là trung điểm của SA. hãy xác định giao điểm của đường thẳng KG và mặt phẳng (ABC)
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng a, gọi G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng (ABC)bằng A.
a
6
9
B.
a
3
6
C.
a
6
6
D.
a
6...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng a, gọi G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng (ABC)bằng
A. a 6 9
B. a 3 6
C. a 6 6
D. a 6 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh AB 2a . Tam giác SAB là tam giác đều và nằm trong mặt phắng vuông góc với đáy. Gọi M là trung điểm SB và N là điểm trên cạnh SC sao cho SC3SN. Tính thể tích V của khối chóp S.AMN. A.
V
2
3
a
3
9
B. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh AB = 2a . Tam giác SAB là tam giác đều và nằm trong mặt phắng vuông góc với đáy. Gọi M là trung điểm SB và N là điểm trên cạnh SC sao cho SC=3SN. Tính thể tích V của khối chóp S.AMN.
A. V = 2 3 a 3 9
B. V = 3 a 3 9
C. V = 3 a 3 3
D. V = 2 3 a 3 3
Đáp án B
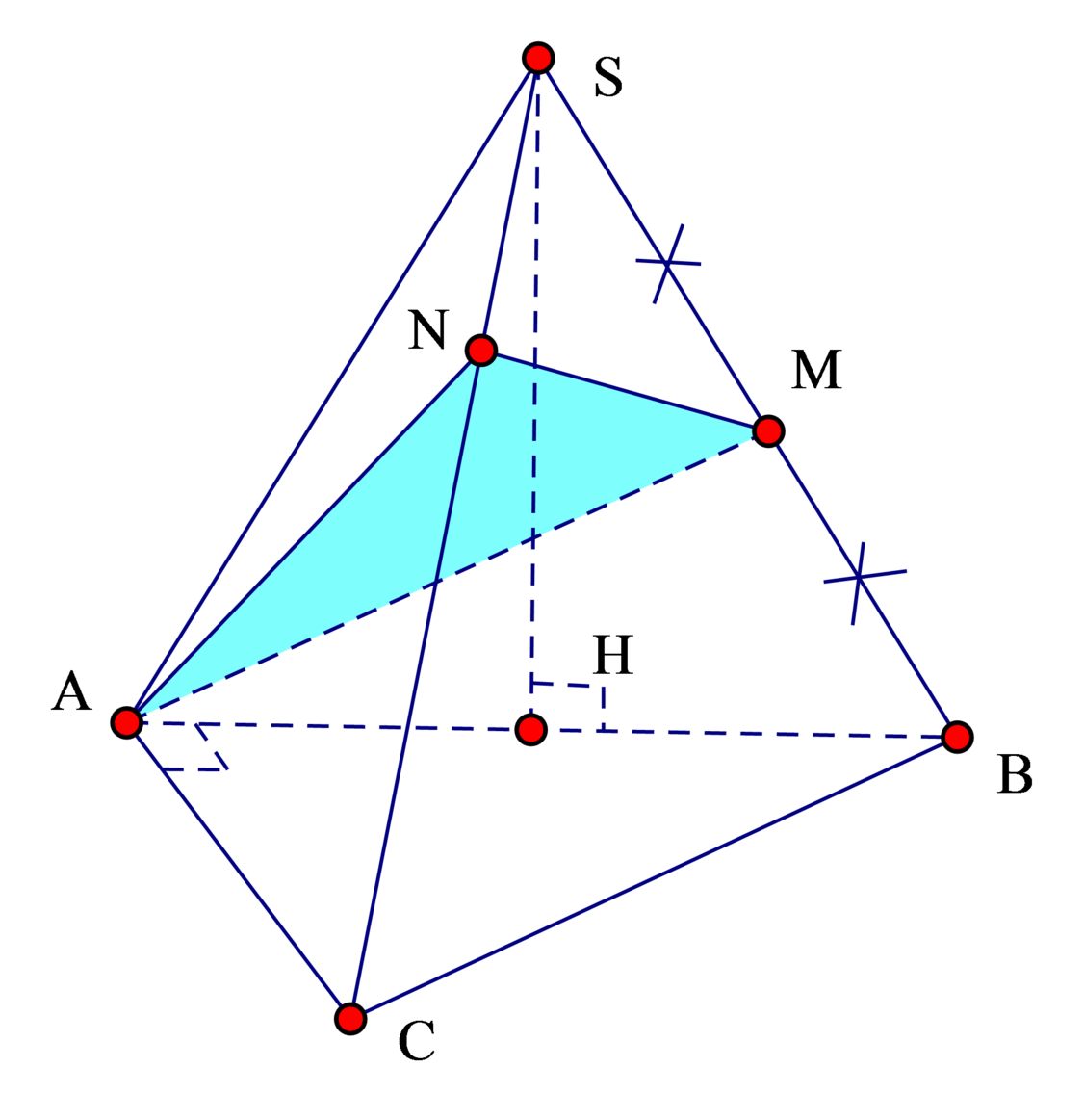
Kẻ đường cao SH trong Δ S A B ⇒ A H ⊥ A B C .
Δ S A B đều ⇒ A H = 2. a 3 2 = a 3
Diện tích tam giác: A B C = 1 2 . 2 a 2 = 2 a 2
⇒ V S . A B C = 1 3 S H . d t A B C = 1 3 a 3 .2 a 2 = 2 a 3 3 3
Ta có: V S . A M N V S . A B C = S M S B . S N S C = 1 2 . 1 3 = 1 6
⇒ V S . A M N = V S . A B C 6 = 2 a 3 3 3.6 = a 3 3 9
Đúng 0
Bình luận (0)
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC
a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC)
b) Tính khoảng cách giữa hai đường thẳng AB và SG
Cho hình chóp S.ABC có tam giác ABC và tam giác SAB là tam giác đều. hình chiếu vuông góc của S trên (ABC) là trung điểm của của AB. SC = (a căn6)/2, gọi M là trung điểm của SC. tính thể tích khối chóp S.ABC và tính khoảng cách giữa AM với SB