Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh AB = 2a . Tam giác SAB là tam giác đều và nằm trong mặt phắng vuông góc với đáy. Gọi M là trung điểm SB và N là điểm trên cạnh SC sao cho SC=3SN. Tính thể tích V của khối chóp S.AMN.
A. V = 2 3 a 3 9
B. V = 3 a 3 9
C. V = 3 a 3 3
D. V = 2 3 a 3 3
Đáp án B
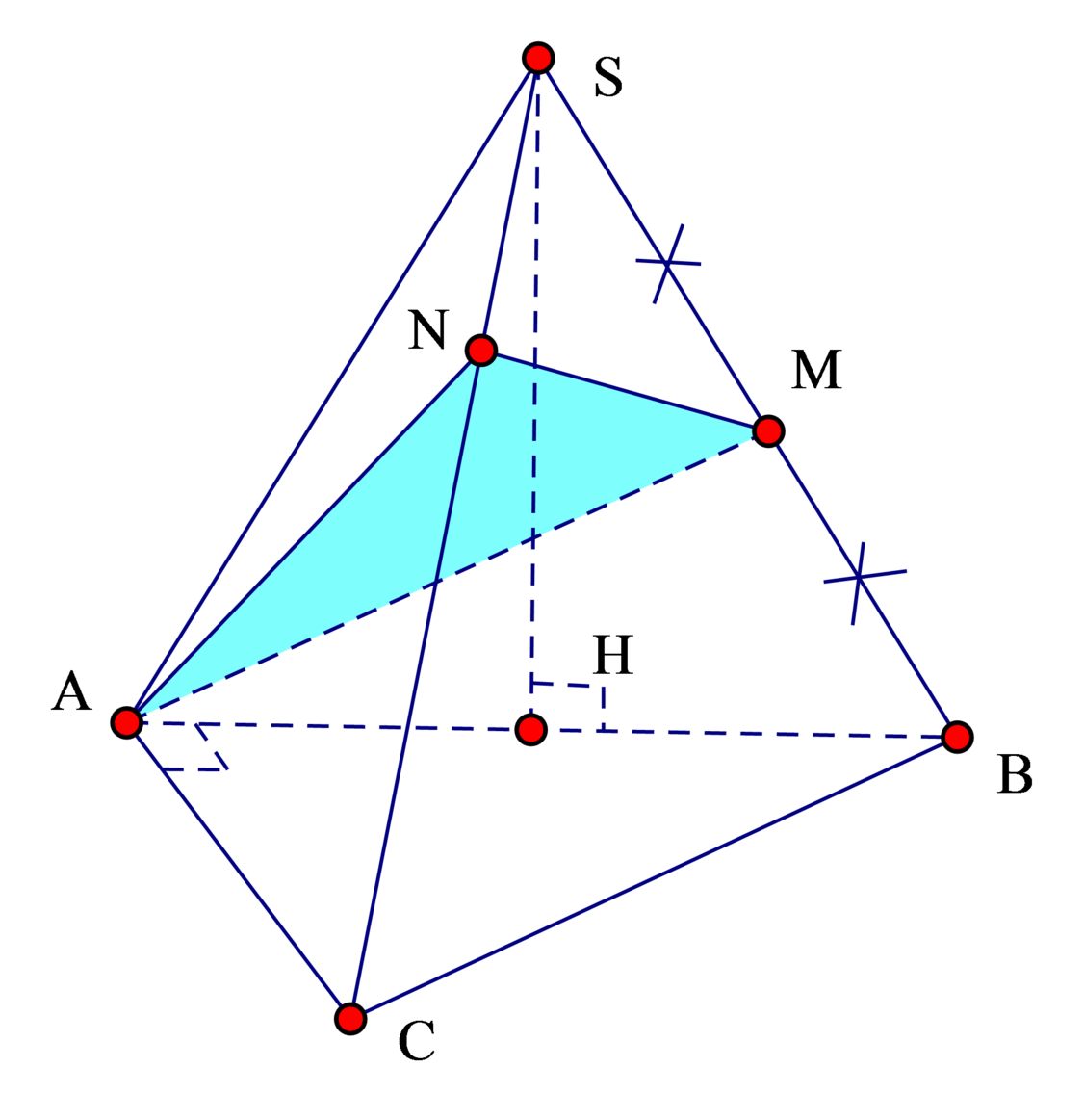
Kẻ đường cao SH trong Δ S A B ⇒ A H ⊥ A B C .
Δ S A B đều ⇒ A H = 2. a 3 2 = a 3
Diện tích tam giác: A B C = 1 2 . 2 a 2 = 2 a 2
⇒ V S . A B C = 1 3 S H . d t A B C = 1 3 a 3 .2 a 2 = 2 a 3 3 3
Ta có: V S . A M N V S . A B C = S M S B . S N S C = 1 2 . 1 3 = 1 6
⇒ V S . A M N = V S . A B C 6 = 2 a 3 3 3.6 = a 3 3 9



