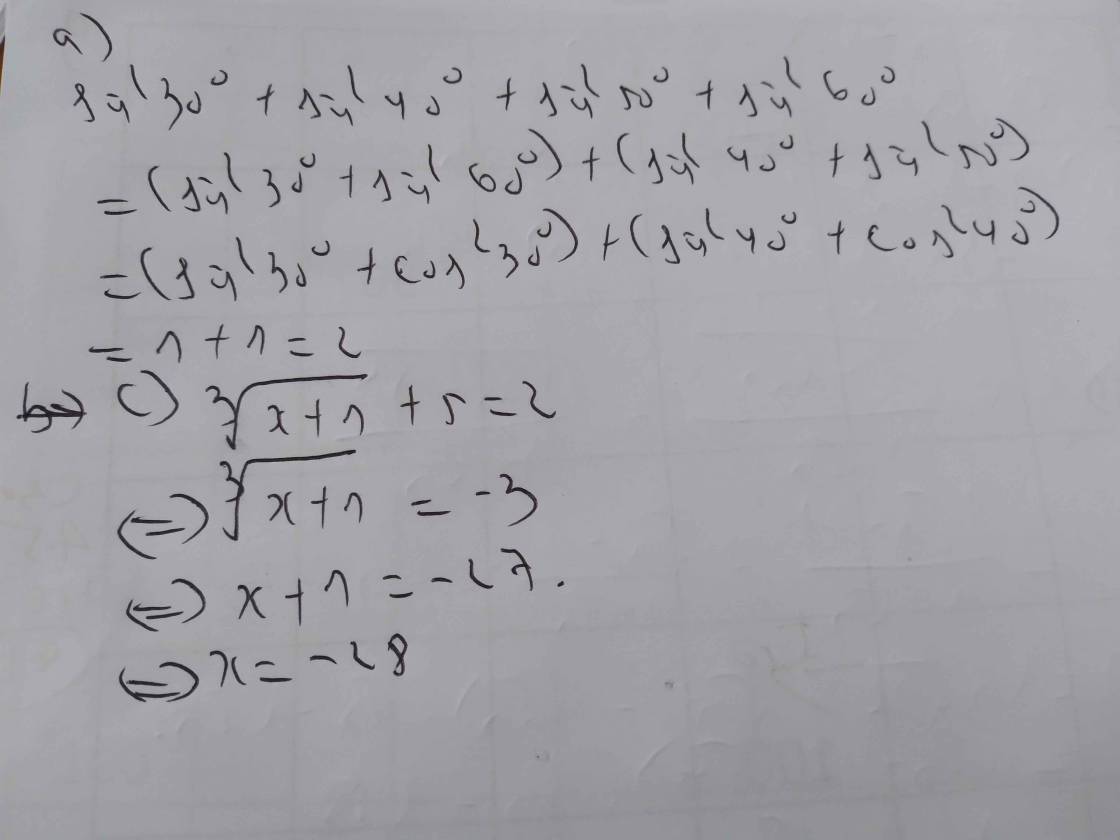c) x² + 9x = 10

x² + 9x - 10 = 0

=> x² - x + 10x - 10 = 0

=> x(x - 1) + 10(x - 1) = 0

=> (x + 10)(x - 1) = 0

=> \(\orbr{\begin{cases}x=-10\\x=1\end{cases}}\)

d) 2x² + 9x = 35

=> 2x² + 9x - 35 = 0

=> 2x² + 14x - 5x - 35 = 0

=> 2x(x + 7) - 5(x + 7) = 0

=> (x + 7)(2x - 5) = 0

=> \(\orbr{\begin{cases}x=-7\\x=\frac{5}{3}\end{cases}}\)

(x² - 2x - 1)² - 5(x² - 2x - 1) - 14 = 0

=> (x² - 2x - 1)² + 2(x² - 2x - 1) - 7(x² - 2x - 1) - 14 = 0

=> (x² - 2x - 1)(x² - 2x + 1) - 7(x² - 2x + 1) = 0

=> (x² - 2x + 1)(x² - 2x - 8) = 0

=> (x - 1)² (x - 4)(x + 2) = 0

=> x = 1 hoặc x = 4 hoặc x = -2

e) (2k² + 5k + 1)² - 12(2k² + 5k + 1) + 32 = 0

=> (2k² + 5x + 1)² - 4(2k² + 5k + 1) - 8(2k² + 5k + 1) + 32 = 0

=> (2k² + 5k + 1)(2k² + 5k - 3) - 8(2k² + 5k - 3) = 0

=> (2k² + 5k - 3)(2k² + 5k - 7) = 0

=> (2k² + 6k - k - 3)(2k² - 2x + 7k - 7) = 0

=> (k + 3)(2k - 1)(k - 1)(2k + 7) = 0

=> k = -3 hoặc k = 1/2 hoặc k = 1 hoặc k = -7/2

1.x² + 6x = 0 < như này nhỉ ? >

⇔ x( x + 6 ) = 0

⇔ x = 0 hoặc x + 6 = 0

⇔ x = 0 hoặc x = -6

2. x² - 25x + 250 = 0

⇔ ( x² - 25x + 625/4 ) + 375/4 = 0

⇔ ( x - 25/2 )² = -375/4 ( vô lí )

=> Phương trình vô nghiệm

3. x² + 9x = 10

⇔ x² + 9x - 10 = 0

⇔ x² - x + 10x - 10 = 0

⇔ x( x - 1 ) + 10( x - 1 ) = 0

⇔ ( x - 1 )( x + 10 ) = 0

⇔ x - 1 = 0 hoặc x + 10 = 0

⇔ x = 1 hoặc x = -10

4. 2x² + 9x = 35

⇔ 2x² + 9x - 35 = 0

⇔ 2x² + 14x - 5x - 35 = 0

⇔ 2x( x + 7 ) - 5( x + 7 ) = 0

⇔ ( x + 7 )( 2x - 5 ) = 0

⇔ x + 7 = 0 hoặc 2x - 5 = 0

⇔ x = -7 hoặc x = 5/2

5. ( x² - 2x - 1 )² - 5( x² - 2x - 1 ) - 14 = 0

Đặt t = x² - 2x - 1

bthuc ⇔ t² - 5t - 14 = 0

          ⇔ t² - 7t + 2t - 14 = 0

          ⇔ t( t - 7 ) + 2( t - 7 ) = 0

          ⇔ ( t - 7 )( t + 2 ) = 0

          ⇔ ( x² - 2x - 1 - 7 )( x² - 2x - 1 + 2 ) = 0

          ⇔ ( x² - 4x + 2x - 8 )( x - 1 )² = 0

          ⇔ ( x - 4 )( x + 2 )( x - 1 )² = 0

          ⇔ x - 4 = 0 hoặc x + 2 = 0 hoặc x - 1 = 0

          ⇔ x = 4 hoặc x = -2 hoặc x = 1

6. ( 2k² + 5k + 1 )² - 12( 2k² + 5k + 1 ) + 32 = 0

Đặt t = 2k² + 5k + 1

bthuc ⇔ t² - 12t + 32 = 0

          ⇔ t² - 8t - 4t + 32 = 0

          ⇔ t( t - 8 ) - 4( t - 8 ) = 0

          ⇔ ( t - 8 )( t - 4 ) = 0

          ⇔ ( 2k² + 5k + 1 - 8 )( 2k² + 5k + 1 - 4 ) = 0

          ⇔ ( 2k² - 2k + 7k - 7 )( 2k² - k + 6k - 3 ) = 0

          ⇔ ( k - 1 )( 2k + 7 )( 2k - 1 )( k + 3 ) = 0

          ⇔ k = 1 hoặc k = -7/2 hoặc k = 1/2 hoặc k = -3

a) \(x⋮15;x⋮35;x⋮42\&250< x< 850\) (sửa dấu chia thành chia hết)

\(BCNN\left(15;35;42\right)=210\)

\(\Rightarrow x\in BC\left(15;35;42\right)=\left\{0;210;420;630;840;...\right\}\)

mà \(250< x< 850\)

\(\Rightarrow x\in\left\{420;630;840\right\}\)

b) x nhỏ nhất khác 0 thỏa mãn \(x⋮15;x⋮115\)

\(BCNN\left(15;115\right)=345\)

Vậy \(x\in\left\{345\right\}\) thỏa mãn đề bài

Bài c bạn xem lại đề

phần c lỗi nha ạ, mình sửa lại 

c) (x−1) chia hết 52,(x−1) chia hết 35 và 1000 < x < 2000

\(a,96-3\left(x+8\right)=42\\ \Rightarrow3\left(x+8\right)=54\\ \Rightarrow x+8=18\\ \Rightarrow x=10.\\ b,15.5\left(x-25\right)-225=0\\ \Rightarrow75\left(x-25\right)-225=0\\ \Rightarrow75\left(x-25\right)=225\\ \Rightarrow x-25=3\\ \Rightarrow x=28.\\ c,250:x+15=25\\ \Rightarrow250:x=10\\ \Rightarrow x=25\\ d,36:\left(x-5\right)=2^2\\ \Rightarrow36:\left(x-5\right)=4\\ \Rightarrow x-5=9\\ \Rightarrow x=14.\\ e,\left[3.\left(70-x\right)+5\right]:2=46\\ \Rightarrow3.\left(70-x\right)+5=92\\ \Rightarrow3\left(70-x\right)=87\\ \Rightarrow70-x=29\\ \Rightarrow x=41.\)

( x - 25) x 17 = 34

=> x - 25 = 34 : 17

     x - 25 = 2

=> x = 2 + 25

     x = 27

145 + (150 - x) = 250

=> 150 - x = 250 - 145

     150 - x = 105

=> x = 150 - 105

     x = 45

(2x - 7) x 81 = 0

=> 2x - 7 = 0 : 81

    2x - 7 = 0

  => 2x = 7

   => x = 7 : 2 = 3,5

x - 90 : 15  = 32

=> x - 6 = 32

=> x = 32 + 6

    x = 38

520 - (x - 5) = 250 : 5

 => 520 - (x - 5) = 50

=> x - 5 = 520 - 50

   x - 5 = 470

=> x = 470 + 5

    x = 475

t i c k nhé!! 346457567684786896789

a ) \(\left(x-5\right).17=34\)

=> \(x-5=2\)

=> \(x=7\)

b ) \(145+\left(150-x\right)=250\)

=> \(150-x=105\)

=> \(x=150-105\)

=> \(x=45\)

c ) \(\left(2.x-7\right).81=0\)

=> \(2x-7=0\)

=> \(2x=7\)

=> \(x=\frac{7}{2}\)

d ) \(x-90:15=32\)

=> \(x-6=32\)

=> \(x=38\)

Mấy cái dấu chấm đó là nhân đó nhé

Chọn B

a. Ta có : 54 = 2 . 33

           12 = 22.3

  Do đó ƯCLN ( 54 , 12 ) = 2 .3 = 6 hay x = 6

Vậy x = 6 

b. x ∈ BC(8, 9) và x nhỏ nhất

=> x là BCNN(8, 9)

Ta có: 8 = 23

           9 = 32

=> BCNN(8, 9) = 23 . 32 = 72

Vậy x = 72. 

c. Vì x chia hết cho 12 và 18

=> x ∈ BC(12;18) = {0;36;72;144;288;...}

Mà x < 250 nên x ∈ {0;36;72;144} 

d. Vì 15 chia hết cho 2x+1

=> 2x+1 là ước tự nhiên của 15

=> 2x+1 thuộc 1,3,5,15

xét 2x+1=1 => x = 0(t/m)

     2x+1=3 => x=1(t/m)

      2x+1 =5 => x=2(t/m)

     2x+1=15 => x=7(t/m)

Vậy x ={ 0;1;2;7}

a) Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích của ít nhất 1 thừa số 5 là: 250, 255, 260, ..., 1990, 1995.

Số các số hạng treong dãy đó là :

   ( 1995 - 250 ) : 5 + 1 = 350 ( số )

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành ít nhất 2 thừa số 5 là : 250, 275, 300, ... , 1950, 1975 

Số các số hạng trong dãy đó là :

    ( 1975 - 250 ) : 25 + 1 = 70 ( số )

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành tích của ít nhất 3 thừa số 5 là : 250, 375, 500, ... , 1725, 1875

Số các số hạng trong dãy đó là :

     ( 1875 - 250 ) : 125 + 1 = 14 ( số )

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành tích của ít nhất 4 thừa số 5 là : 625, 1250, 1875

Tích trên có thể phân tích thành số thừa số 5 là :

      350 + 70 + 14 + 3 = 437 ( thừa số )

Mỗi thừa số 5 nhân với 1 số chẵn cho ta một số tận cùng là một chữ số 0.

Vậy có 437 chữ số 0 ở tận cùng của tích trên

Đáp số : 437 chữ số 0.

b) Theo bài ra ta có dãy tính sau: 1 x 2 x 3 x ... x 2014 x 2015

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành tích của ít nhất một thừa số 5 là : 5 ; 10 ; 15 ; ... ; 2010; 2015 

Số các số hạng trong dãy đó là :

   ( 20915 - 5 ) : 5 + 1 = 403 ( số ) 

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành tích của ít nhất 2 thừa số 5 là : 25; 50 ; 75 ; ... ; 1975; 2000 

Số các số hạng trong dãy đó là :

    ( 2000 - 25 ) : 25 + 1 = 80 ( số )

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành tích của ít nhất 3 thừa số 5 là : 125; 250; 375; ... ; 1875; 2000

Số các số hạng trong dãy đó là :

     ( 2000 - 125 ) : 125 + 1 = 16 ( số)

Trong tích trên có các thừa số chia hết cho 5 mà ta có thể phân tích thành tích của ít nhất 4 thừa số 5 là : 625; 1250; 1875

Tích trên có thể phân tích thành số thừa số 5 là :

    403 + 80 + 16 + 3 = 502 ( thừa số )

Mỗi thừa số 5 nhân với 1 số chẵn cho ta một số có tận cùng là một chữ số 0

Vậy có 502 chữ số 0 ở tận cùng của tích trên

Đáp số : 502 chữ số 0

Cbht