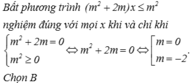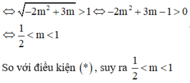gọi m là giá trị để bất phương trình x+4m^2>=2mx+1 là[-5; vô cực] giá trị m thu vào khoảng

Những câu hỏi liên quan
Cho hệ bất phương trình
m
x
2
-
x
-
5
≤
0
(
1
-
m
)
x...
Đọc tiếp
Cho hệ bất phương trình m x 2 - x - 5 ≤ 0 ( 1 - m ) x 2 + 2 m x + m + 2 ≥ 0 . Các giá trị của x thỏa mãn hệ bất phương trình khi m = 1 là:
A. S = 1 - 2 21 2 ; 1 + 2 21 2
B. S = 1 - 3 21 2 ; 1 + 3 21 2
C. S = 1 - 4 21 2 ; 1 + 4 21 2
D. S = 1 - 21 2 ; 1 + 21 2
Chọn D.
Với m = 1 hệ bất phương trình trở thành:
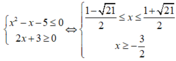
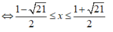
Vậy tập nghiệm hệ bất phương trình là
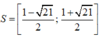
Đúng 0
Bình luận (0)
Cho phương trình x^2 -2mx+4m-4=0 (1) , m là tham số
a)Gia phương trình với m=1
b)Tìm giá trị của m để phương trình (1) có hai nghiệm phân biệt x1,x2 thỏa mãn điều kiện x1^2 +2mx2 -8m+5=0
1. Cho phương trình x2 -2mx-4m-5=0 (x là ẩn số, m là tham số). a) Chứng minh rằng phương trình luôn luôn có nghiệm với mọi m. b) Gọi x1, x2 là các nghiệm của phương trình. Tìm m để biểu thức A = đạt giá trị nhỏ nhất.
\(a,\Delta'=\left(-m\right)^2-\left(4m-5\right)=m^2-4m+5=\left(m^2-4m+4\right)+1=\left(m-2\right)^2+1>0\)
Vậy pt luôn có 2 nghiệm phân biệt với mọi m
câu b thiếu
Đúng 1
Bình luận (0)
Bài 1. Tìm m để f (x)=mx^2 -2(m-1)x+4m-1 luôn dương Bài 2 tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm đúng với mọi a.5x^2-x+m>0 b.m(m+2)x^2+2mx+2>0
Gọi n là số các giá trị của tham số m để bất phương trình
2
m
-
4
x
3
+
2
x
2
+
m
2
-
3
m
+...
Đọc tiếp
Gọi n là số các giá trị của tham số m để bất phương trình 2 m - 4 x 3 + 2 x 2 + m 2 - 3 m + 2 x 2 + 2 x - m 3 - m 2 - 2 m x + 2 < 0 vô nghiệm. Giá trị của n bằng:
A. 5
B. 1
C. 4
D. 2
1. Tập tất cả các giá trị của tham số m để bất phương trình
m
2
+
2
m
x
≤
m
2
nghiệm đúng với mọi x là: A.
-
2
;
0
B.
-
2
;
0...
Đọc tiếp
1. Tập tất cả các giá trị của tham số m để bất phương trình m 2 + 2 m x ≤ m 2 nghiệm đúng với mọi x là:
A. - 2 ; 0
B. - 2 ; 0
C. 0
D. - 2 ; 0
giả sử x1,x2 là 2 nghiệm của phương trình: x2-2mx+m2-1=0
Hãy tìm các giá trị của m để bất đẳng thức sau đúng:
\(3\sqrt{x_1x_2-x_1-x_2+2}-\sqrt{x^2_1+x^2_2+2m^2-4m-1}\ge2\)
tìm m để phương trình (m+1)x2 + 2(m+3)x - m+2 =0 có 2 nghiệm phân biệt
tìm các giá trị của tham số m để bất phương trình (m2 - 4m -5)x2 +2(m-5)x-1\(\ge0\) vô nghiệm
a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)
Đúng 0
Bình luận (0)
Cho bất phương trình
x
2
+
2
x
+
m
+
2
m
x
+
3
m
2
-
3
m
+
1
0
với m là tham số. Tập tất cả giá trị của m để bất phương trình có nghiệm là
a
;
b...
Đọc tiếp
Cho bất phương trình x 2 + 2 x + m + 2 m x + 3 m 2 - 3 m + 1 < 0 với m là tham số. Tập tất cả giá trị của m để bất phương trình có nghiệm là a ; b c . Tính a + b + c
A. a + b + c = 4
B. a + b + c = 0
C. a + b + c = 1
D. a + b + c = 2