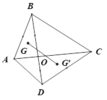
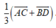Cho tứ giác ABCD. Gọi O là giao điểm của 2 đường chéo AC và BD; I, J lần lượt là trung điểm của AB và CD. Giả sử H, K lần lượt là trực tâm của các tam giác OAD và OBC. Chứng minh rằng \(IJ\perp HK\)

Những câu hỏi liên quan
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Gọi chu vi tứ giác ABCD là PABCD Chứng minh
a)AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b)Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . gọi chu vi của tứ giác ABCD là PABCD . chứng minh
a) AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b) Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
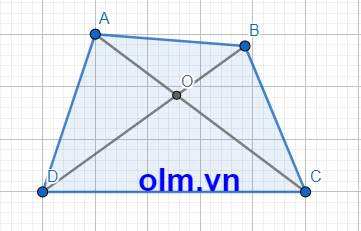
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
Đúng 0
Bình luận (0)
cho tứ giác ABCD gọi O là giao điểm của hai đường chéo AC và BD gọi chu vi của tứ giác ABCD là P
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Chứng minh :
a) AC+BD>AB+CD
b)AC+BD>AD+ BC
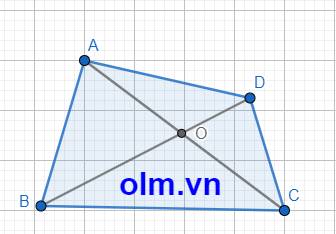
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD
Đúng 2
Bình luận (0)
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Chứng minh :
a) AC+BD>AB+CD
b)AC+BD>AD+ BC
(dùng bất đẳng thức tam giác)
a)
Ta có
OA + OB > AB ( Bất đẳng thức tam giác )
OC + OD > CD ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OB + OC +OD > AB + CD
=> AC + BD > AB + CD
Bài toán được chứng minh
b)
Ta có:
OA + OD > AD ( Bất đẳng thức tam giác )
OC + OB > CB ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OD + OC + OB > AD + CB
=> AC + BD > AD + BC
Bài toán được chứng minh
Đúng 0
Bình luận (0)
Bài 3. Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. CMa, AC+BDAB+CDb, AC+BDAD+BCBài 4. Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Gọi chu vi của tứ giác ABCD là P_{ABCD}Cma,AC+BDfrac{P_{ABCD}}{2}b, Nếu ACfrac{P_{ABCD}}{2}thì AC+BDP_{ABCD}giúp minh nhanh nhanh nha mình tick cho .......ahihi!
Đọc tiếp
Bài 3. Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. CM
a, AC+BD>AB+CD
b, AC+BD>AD+BC
Bài 4. Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Gọi chu vi của tứ giác ABCD là \(P_{ABCD}\)Cm
a,AC+BD>\(\frac{P_{ABCD}}{2}\)
b, Nếu AC<\(\frac{P_{ABCD}}{2}\)thì AC+BD<\(P_{ABCD}\)
giúp minh nhanh nhanh nha mình tick cho .......ahihi!
Hi vọng bạn có kiến thức vững về BĐT tam giác nha, mấy bài này toàn BĐT tam giác thoi, mình ko chứng minh lại đâu.
Bài 3:
a) Xét tam giác AOB: \(OB>AB-AO\)
Xét tam giác DOC: \(OD>DC-OC\)
Cộng vế theo vế: \(OB+OD>AB+DC-\left(AO+OC\right)\Leftrightarrow BD>AB+DC-AC\Leftrightarrow BD+AC>AB+DC\)
b) Hoàn toàn tương tự với 2 tam giác AOD và BOC:
\(\Rightarrow\hept{\begin{cases}OD>AD-AO\\OB>BC-OC\end{cases}\Rightarrow BD>AD+BC-AC\Leftrightarrow BD+AC>AD+BC}\)
Bài 4:
a) Từ câu 3 ta có \(\hept{\begin{cases}BD+AC>AB+CD\\BD+AC>AD+BC\end{cases}}\)Cộng vế theo vế:
\(\Rightarrow2\left(BD+AC\right)>AB+BC+CD+DA=P_{ABCD}\Rightarrow BD+AC>\frac{P_{ABCD}}{2}\)
b) Câu này thực ra không cần đề cho trước \(AC< \frac{P_{ABCD}}{2}\)đâu, vì đây là điều hiển nhiên mà
Xét 2 tam giác ABC và ADC: \(\hept{\begin{cases}AC< AB+BC\\AC< AD+DC\end{cases}}\)cộng vế theo vế:
\(\Rightarrow2AC< AB+BC+CD+DA=P_{ABCD}\Rightarrow AC< \frac{P_{ABCD}}{2}\)(1)
Hoàn toàn tương tự với 2 tam giác ABD và CBD \(\Rightarrow BD< \frac{P_{ABCD}}{2}\)(2)
Cộng (1) và (2) vế theo vế: \(AC+BD< P_{ABCD}\)
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất. A. OA + OB + OC + OD
AB + BC + CD + DA. B.
A
B
+
B
C
+
C
D
+
D
A
2
O
A
+
O
B
+...
Đọc tiếp
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất.
A. OA + OB + OC + OD < AB + BC + CD + DA.
B. A B + B C + C D + D A 2 < O A + O B + O C + O D .
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Đáp án cần chọn là:C
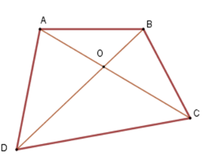
+ Xét tam giác OAB ta có OA + OB > AB (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có OC + OD > CD; OB + OC > BC; OA + OD > AD
Cộng vế với vế ta được
OA + OB + OC + OD + OB + OC + OA + OD > AB + BC + CD + AD
⇔ 2(OA + OB + OC + OD) > AB + BC + CD + DA
⇔ OA + OB + OC + OD > A B + B C + C D + D A 2 nên B đúng
+ Xét tam giác ABC có AB + BC > AC (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có BC + CD > BD; CD + DA > AC; AD + DB > BD
Cộng vế với vế ta được
AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD
⇔ 2(AB + BC + CD + DA) > 2(AC + BD)
⇔ AB + BC + CD + DA > AC + BD mà AC + BD = OA + OC + OB + OD nên
OA + OB + OC + OD < AB + BC + CD + DA nên A đúng
Vậy cả A, B đều đúng.
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB=BC=CD và BAD+ADC=140. Gọi O là giao điểm của 2 đường chéo AC và BD. Tính góc AOD
Cho tứ giác ABCD nôị tiếp đường tròn tâm O, đường kính AD. GỌi I là giao điểm 2 đường chéo AC và BD. Gọi H là hình chiếu vuông góc của điểm I lên AD và M là trung điểm của đoạn Di.
GỌi P là giao điểm của BC và HM. Chứng minh rằng: TỨ giác BCMH nội tiếp đường tròn
Cho tứ giác ABCD ; gọi O là giao điểm của hai đường chéo AC và BD. Gọi G ; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó
G
G
→
bằng: A. B. C. D.
Đọc tiếp
Cho tứ giác ABCD ; gọi O là giao điểm của hai đường chéo AC và BD. Gọi G ; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó G G ' → bằng:
A. 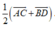
B. 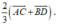
C. ![]()
D.