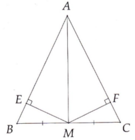
cho tam giacs abc cân tại a,m là trung điểm của bc chứng minh rằng am vuông góc với bc

Những câu hỏi liên quan
Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.
Đúng 0
Bình luận (2)
Cho tam giác ABc cân tại A. M là trung điểm cạnh BC. Chứng minh rằng AM vuông góc với BC
Vì tam giác ABC cân tại A suy ra AB=AC
Vì M là trung điểm BC suy ra BM=CM
Xét tam giác AMB và tam giác AMC có
AB=AC
cạnh AM chung
BM=CM
suy ra tam giác AMB =tam giác AMC (c.c.c)
suy ra góc AMC=góc AMB(hai góc tương ứng)
Mà góc AMC+góc AMB=180 độ
suy ra góc AMC bằng góc AMB=90 độ
suy ra AM vuông góc với BC
Đúng 0
Bình luận (0)
ghi cái định lí Pain vào vở đê
định lĩ six path or Pain : trong tam giác Cân đường trung tuyến ở đỉnh góc cân cắt cạnh đối diện tại 1 điểm bất kì thì suy ra nó vừa là trung tuyến Phân giác trung trực "
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Gọi E là trung điểm của BC. M là điểm bất kì thuộc cạnh BC (M khác E). Kẻ BH vuông góc với AM tại H và CK vuông góc với AM tại K.
a) Chứng minh △KAC = △HBA
b) Chứng minh AE vuông góc với BC.
c) Tam giác KEH là tam giác gì? Vì sao?
b: Ta có: ΔABC cân tại A
mà AE là đường trung tuyến
nên AE là đường cao
Đúng 0
Bình luận (0)
tam giác ABC cân tại A gọi AM vuông góc với BC a)Chứng minh rằng M là đường trung trực của đoạn BC
b) Về phía ngoài tam giác ABC lấy điểm D sao cho DB = BC chứng minh A,M,d mặt thẳng hànga: ΔABC cân tại A
mà AM là đường cao
nên AM là trung trực của BC(1)
b: DB=DC
nên D nằm trên trung trực của BC(2)
(1), (2) =>A,M,D thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn dựng phía ngoài tam giác 2 tam giác vuông cân tại A là tam giác ABD và tam giác ACE gọi M là trung điểm của DE chứng minh rằng
a) AM vuông góc với BC và AM=1/2 BC
b) Gọi P là trung điểm của BD; Q là trung điểm của EC và I là trung điểm của BC Tính góc IPQ
c) Chứng minh AI vuông góc với DE
Cho tam giác ABC có góc nhọn tại A. Vẽ bên ngoài tam giác ABC các tam giác vuông cân đỉnh A là ABD và ACE. Gọi M là trung điểm của BC. Chứng minh rằng AM vuông góc với DE.
Cho tam giác ABC cân tại A . Gọi M là trung điểm của BC. Chứng minh AM vuông góc với BC
AB = AC nên A nằm trên đường trung trực của BC.
MB = MC nên M cũng vậy
Suy ra AM là trung trực của BC do đó AM vuông góc BC.
Đúng 0
Bình luận (0)
Tam giác ABC cân có M là trung điểm ==> AM là trung tuyến của tam giác ABC
Mà trong tam giác cân, đường trang tuyến là đường cao ==> AM vuông góc với BC
Đúng 0
Bình luận (0)
Xét t/g AMB và t/g AMC có :
MB = MC ( M là trung điểm của BC)
Góc B = góc C ( t/ g ABC cân tại A)
AB = AC ( t/g ABC cân tại A)
Suy ra t/g AMB = t/g AMC ( c. g. c)
Suy ra góc BMA = góc CMA ( 2 góc t/ ứng)
Mà góc BMA + góc CMA = 180 độ ( 2 góc kề bù) suy ra BMA = 90 độ
Suy ra AM vuông góc với BC ( đpcm)
Bn tự vẽ hình nha . Chúc bn hok tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC nhọn dựng phía ngoài tam giác 2 tam giác vuông cân tại A là tam giác ABD và tam giác ACE gọi M là trung điểm của DE chứng minh rằng
a) AM vuông góc với BC và AB=AM=1/2 BC
b) Gọi P là trung điểm của BD; Q là trung điểm của EC và I là trung điểm của BC Tính góc IPQ
c) Chứng minh AI vuông góc với DE
Cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh:
a) AM là trung trực của của BC;
b) ME = MF và AM là trung trực của EF;
c) EF// BC.
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
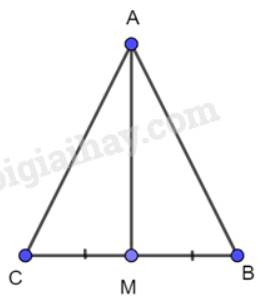
Xét 2 tam giác AMB và AMC có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
\(\Rightarrow\) \(\Delta AMB=\Delta AMC\) (c.c.c)
\(\Rightarrow\) \(\widehat {BAM} = \widehat {CAM}\)(2 góc tương ứng).
Mà tia AM nằm trong góc BAC
\(\Rightarrow\) AM là phân giác của góc BAC
Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\)(2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
Nên: \(\widehat {AMB} = \widehat {AMC} = {90^o}\).
Vậy AM vuông góc với BC.
Đúng 0
Bình luận (0)