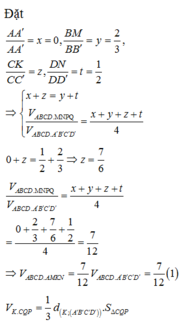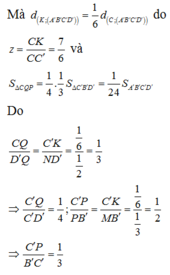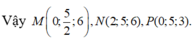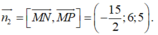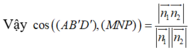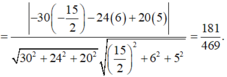Cho hình hộp ABCD.A'B'C'D'. Gọi M,N thứ tự là trung điểm CD và DD'; G và G' lần lượt là trọng tâm tứ diện A'D'MN và BCC'D'. Chứng minh rằng đường thẳng GG' và mặt phẳng (ABB'A') song song với nhau

Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, AA'=c. Gọi M và N theo thứ tự là trung điểm của A'B' và B'C'
Tính tỉ số giữa thể tích khối chóp D'DMN và thể tích khối hộp chữ nhật ABCD.A'B'C'D' ?
Cho hình hộp
A
B
C
D
.
A
B
C
D
có thể tích bằng 1. Gọi M là điểm thỏa mãn
B
M
→
2
3
B
B
→
và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai ph...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có thể tích bằng 1. Gọi M là điểm thỏa mãn B M → = 2 3 B B ' → và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
A. 67 144
B. 4 9
C. 3 8
D. 181 432
Chọn D.
Phương pháp:

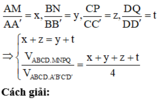
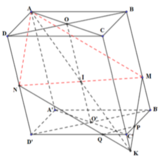
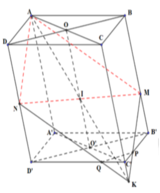
Gọi O, O’ lần lượt là tâm của các hình bình hành ABCD, A’B’C’D’.
Trong (BDD’B’), gọi I là giao điểm của OO’ và MN
Trong (ACC’A’), gọi K là giao điểm của AI và CC’
Trong (CDD’C’), gọi Q là giao điểm của NK và C’D’
Trong (CBB’C’), gọi P là giao điểm của MK và C’B’
=> Thiết diện của hình hộp cắt bởi mặt phẳng (AMN) là ngũ giác AMPQN.
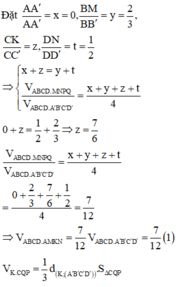
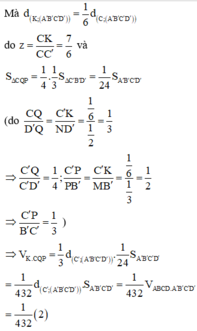
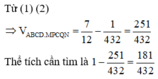
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.ABCD có thể tích bằng 1. Gọi M là điểm thỏa mãn
B
M
→
2
3
B
B
→
và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có thể tích bằng 1. Gọi M là điểm thỏa mãn B M → = 2 3 B B ' → và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
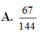
![]()
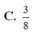
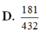
Cho hình hộp ABCD.A'B'C'D'. Gọi E và F theo thứ tự là trung điểm của các cạnh BB' và DD'. Mặt phẳng (CEF) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó ?
Trước hết, ta xác định thiết diện của hình hộp ABCD.A’B’C’D’ khi cắt bởi mp (CEF). Mặt phẳng (CEF) chứa đường thẳng EF mà E là trung điểm của BB’, F là trung điểm của cơ nên EF chứa giao điểm O của các đường chéo hình hộp, do đó mặt phẳng (CEF) cùng chứa giao điểm O của các đường chéo và nó cũng chứa đường chéo A’C của hình hộp. Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành CEA’F. Qua EF ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt AA’ ở p và cắt CC’ ở Q.
ta có thể tích của hình hộp ABCD.PEQF là: VABCD.PEQF =1/2 VABCD.A’B’C’D’ (1)
Ta cũng chứng minh được một cách dễ dàng: VCFQE = VA’FPE (2) (Hai hình chóp CFQE và A’FPE có chiều cao bằng nhau và diện tích đáy bằng nhau).
Xét khối đa diện ABCDE’F do mặt phẳng (CEF) chia ra trên hình hộp p ABCD.A’B’C’D ta có: VABCD.FA’EQ = VABCD.FPE +VA’FPE (3)
Từ (1), (2), (3) suy ra: VABCD.FA’EQ = 1/2 VABCD.A’B’C’D’ Vậy mặt phẳng (CEF) chia hình hộp thành hai khối đa diện có thể tích bằng nhau, tỉ số của chúng là 1. Chú ý: Có thể lí luận như sau: Giao điểm O của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng (CEF) chứa điểm o nên chia hình hộp thành hai hình đối xứng với nhau qua điểm o. Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.
Đúng 0
Bình luận (0)
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA',A'D'\). Tính góc giữa các cặp đường thẳng:
a) \(MN\) và \(DD'\);
b) \(MN\) và \(CD'\);
c) \(EF\) và \(CC'\).
tham khảo:

a) Trong tam giác ABC có MN là đường trung bình nên MN//AC
Mà AA' // DD'
Nên góc giữa MN và DD' là góc giữa AC Và AA'
b) Vì MN//AC nên góc giữa MN và CD' là góc giữa AC và CD'
c) Trong tam giác AA'D' có EF là đường trung bình nên EF//AD'
Mà CC'//AA'
Nên góc giữa EF và CC' là góc giữa AA' và AD'
Đúng 1
Bình luận (0)
Cho hình hộp ABCD.A'B'C'D'. Xét M thuộc BB', N thuộc Cd sao cho BM : MB' = CN : ND và gọi I, J theo thứ tự là trungd diểm BC, D'A'. Chứng minh rằng M, N, I, J đồng phẳng.
Do \(\frac{BM}{MB'}=\frac{CN}{ND}\) nên \(\frac{BM}{BB'}=\frac{CN}{CD}=t\) với \(t\in\left(0;1\right)\) nào đó
Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AD}=\overrightarrow{b}\) và \(\overrightarrow{AA'}=\overrightarrow{c}\)
Khi đó :
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{a}+t\overrightarrow{c}\)
\(\overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}=\left(1-t\right)\overrightarrow{a}+\overrightarrow{b}\)
\(\overrightarrow{AI}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
\(=\overrightarrow{AA'}+\overrightarrow{A'J}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{c}\)
Suy ra :
\(\overrightarrow{MN}=-t.\overrightarrow{a}+\overrightarrow{b}-t.\overrightarrow{c}\) ; \(\overrightarrow{MI}=\frac{1}{2}\overrightarrow{b}-t\overrightarrow{c}\) và \(\overrightarrow{MJ}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}+\left(1-t\right).\overrightarrow{c}\)
Từ đó, do
\(-t.\overrightarrow{a}+\overrightarrow{b}-t.\overrightarrow{c}=\left(2-t\right).\left(\frac{1}{2}.\overrightarrow{b}-t.\overrightarrow{c}\right)+t.\left(-\overrightarrow{a}\right)+\frac{1}{2}.\overrightarrow{b}+\left(1-t\right).\overrightarrow{c}\)
Nên :
\(\overrightarrow{MN}=\left(2-t\right).\overrightarrow{MI}+t.\overrightarrow{MJ}\)
Suy ra M, N, I, J đồng phẳng
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AB4 AD 5 AA6 . Gọi M , N , P lần luợt là trung điểm các cạnh AD, CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và bằng (MNP) A.
181
469
B.
120
13
469
C.
19
469...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4 AD =5 AA'=6 . Gọi M , N , P lần luợt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và bằng (MNP)
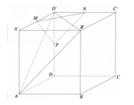
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Cho hình hộp chữ nhật ABCD.ABCD có AB 4, AD 5, AA 6. Gọi M, N, P lần lượt là trung điểm các cạnh AD, CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và (MNP) bằng A.
181
469
B.
120
13
469
C.
19
469...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB =4, AD = 5, AA' =6. Gọi M, N, P lần lượt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và (MNP) bằng
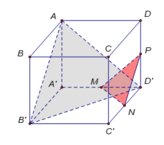
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Chọn A
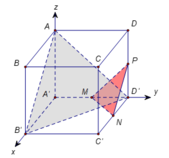
Đối với những bài cồng kềnh và tính toán rất phức tạp
thế này thì nên tọa độ hóa giải rất nhanh, khỏi phải mất nhiều
thời gian và tư duy. Gắn trục tọa độ Oxyz như hình vẽ bên với
A'(0;0;0), D(0;5;6), C' (4;5;0)
![]()
![]()
![]()
![]()
![]()
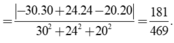
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AB4,AD5,AA6. Gọi M , N , P lần luợt là trung điểm các cạnh AD,CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và (MNP) bằng A.
181
469
B.
120
13
469
C.
19
469
D.
60
61
469
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4,AD=5,AA'=6. Gọi M , N , P lần luợt là trung điểm các cạnh A'D',C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và (MNP) bằng
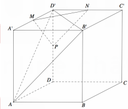
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469