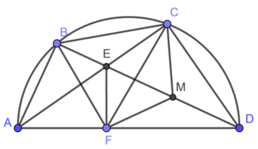
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AD (B thuộc cung nhỏ AC). Gọi giao điểm hai đường chéo AC và BD là H. Kẻ HK vuông góc với AD tại K. Tia BK cắt (O) tại điểm thứ hai là F. Gọi P, Q lần lượt là hình chiếu vuông góc của F trên các đường thẳng AB, BD. Chứng minh CF//HK và PQ đi qua trung điểm của CF.

Những câu hỏi liên quan
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD ( F thuộc AD)
a) CMR : tia CA là tia phân giác góc BCF
b) Gọi M là trung điểm của DE. CMR: CM.BD= DF.DO
Cho tứ giác ABCD nội tiếp nửa đường tròn (O) đường kính AD, hai đường chéo AC và BD cắt nhau tại H. Gọi E là chân đường vuông góc kẻ từ H đến AD.
1. CH/m các tứ giác ABHE và DCHE nội tiếp.
2. C/m EH là đường phân giác góc BEC.
3. Gọi M là giao điểm của hai tia AB và DC chứng minh 3 điểm M,H,E thẳng hàng.
Cho đường tròn (O: R) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm K thuộc cung nhỏ AC, kẻ KH vuông góc AB tại H. Tia AC cắt HK tại I, tia BC cắt HK tại E, nối AE cắt đường tròn (O; R) tại F.
1. Chứng minh tứ giác BHFE là tứ giác nội tiếp.
2. Chứng minh: EF EA EC EB . . .
3. Tính theo R diện tích FEC khi H là trung điểm của OA.
4. Cho K di chuyển trên cung nhỏ AC. Chứng minh đường thẳng FH luôn đi qua một điểm cố định.
giúp mình ý 3 với ạ
Đọc tiếp
Cho đường tròn (O: R) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm K thuộc cung nhỏ AC, kẻ KH vuông góc AB tại H. Tia AC cắt HK tại I, tia BC cắt HK tại E, nối AE cắt đường tròn (O; R) tại F.
1. Chứng minh tứ giác BHFE là tứ giác nội tiếp.
2. Chứng minh: EF EA EC EB . . .
3. Tính theo R diện tích FEC khi H là trung điểm của OA.
4. Cho K di chuyển trên cung nhỏ AC. Chứng minh đường thẳng FH luôn đi qua một điểm cố định.
giúp mình ý 3 với ạ
Cho tứ giác ABCD nội tiếp nửa đường tròn tâm O đường kính AD 2R(AB CD) . Gọi E là giao điểm của hai đường chéo AC và BD, kẻ EF vuông góc với AD tại F. 3/ Gọi I là giao điểm của OC và BF. Chứng minh IB.IFIO.IC 4/ Giả sử. góc BDA 30 độ. Tính theo R thể tích của hình sinh ra khi cho tam giác ABD quay một vòng quanh cạnh AB. giúp e voi mng ơii
Đọc tiếp
Cho tứ giác ABCD nội tiếp nửa đường tròn tâm O đường kính AD = 2R(AB > CD) . Gọi E là giao điểm của hai đường chéo AC và BD, kẻ EF vuông góc với AD tại F. 3/ Gọi I là giao điểm của OC và BF. Chứng minh IB.IF=IO.IC 4/ Giả sử. góc BDA = 30 độ. Tính theo R thể tích của hình sinh ra khi cho tam giác ABD quay một vòng quanh cạnh AB.
giúp e voi mng ơii
3: Xét ΔIOD và ΔIBC có
góc ICB=góc IDO
góc OID=góc BIC
=>ΔIOD đồng dạng với ΔIBC
=>IO/IB=ID/IC
=>IO*IC=IB*ID
Đúng 0
Bình luận (1)
Cho tứ giác $ABCD$ nội tiếp đường tròn đường kính $AD$. Hai đường chéo $AC$ và $BD$ cắt nhau tại $E$. Gọi $F$ là điểm thuộc đường thẳng $AD$ sao cho $EF$ vuông góc với $AD$. Đường thẳng $CF$ cắt đường tròn đường kính $AD$ tại điểm thứ hai là $M$. Gọi $N$ là giao điểm của $BD$ và $CF$. Chứng minh rằng:
a) $CEFD$ nội tiếp đường tròn.
b) $FA$ là đường phân giác của góc $BFM$.
c) $BD.NE BE.ND$.
Đọc tiếp
Cho tứ giác $ABCD$ nội tiếp đường tròn đường kính $AD$. Hai đường chéo $AC$ và $BD$ cắt nhau tại $E$. Gọi $F$ là điểm thuộc đường thẳng $AD$ sao cho $EF$ vuông góc với $AD$. Đường thẳng $CF$ cắt đường tròn đường kính $AD$ tại điểm thứ hai là $M$. Gọi $N$ là giao điểm của $BD$ và $CF$. Chứng minh rằng:
a) $CEFD$ nội tiếp đường tròn.
b) $FA$ là đường phân giác của góc $BFM$.
c) $BD.NE = BE.ND$.
cho tứ giác ABCD nội tiếp (O), đường kính AD (B thuộc cung nhỏ AC). gọi giao điểm hai dduongf chéo AC và BD tại H, kè HK vuông góc với AD tại K. tia BK cắt CD tại điểm thứ hai F. gọi P và Q lần lượt là hình chiếu vuông góc của F trên các dường thẳng AB, CD. chứng minh:CF//HK và PQ đi qua trung điểm của CF
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc AD tại F. Gọi K là trung điểm DE. Chứng minh:a) CA là phân giác góc BCFb) Tứ giác BCKF nội tiếpc) Đường tròn qua 3 điểm K, F, D cắt (O) tại N. P là giao điểm BC và FK. Chứng minh P, D, N thẳng hàng.các ban làm tới câu c) chỉ tớ với {câu a, b ko cần trình bày cx đc)
Đọc tiếp
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc AD tại F. Gọi K là trung điểm DE. Chứng minh:
a) CA là phân giác góc BCF
b) Tứ giác BCKF nội tiếp
c) Đường tròn qua 3 điểm K, F, D cắt (O) tại N. P là giao điểm BC và FK. Chứng minh P, D, N thẳng hàng.
các ban làm tới câu c) chỉ tớ với {câu a, b ko cần trình bày cx đc)
Cho tứ giác ABCD nội tiếp đường tròn tâm O đường kính AD hai đường chéo AC và BD cắt nhau tại I kẻ IE vuông góc với ad A : CM DC ie nội tiếp B: ca là tia phân giác của góc bce C: gọi K là tâm của đường tròn ngoại tiếp tam giác CIE,CM : kbd thẳng hàng
a: góc IED+góc ICD=180 độ
=>IEDC nội tiếp
b: góc ECI=góc BDA=1/2*sđ cung BA
=>góc ECI=góc BCI
=>CI là phân giác của góc BCE
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng: Tia CA là tia phân giác của góc BCF