Cho \(\Delta\)ABC vuông cân tại A. Kẻ tia phân giác của góc A cắt BC tại H. Trên tia AB, AC lấy điểm N và M sao cho BN=AM. Chứng minh rằng:
a, \(\Delta\)AHN=\(\Delta\)CHM
b, \(\Delta\)AHM=\(\Delta\)BHN
c, \(\Delta\)MHN vuông cân
Cho \(\Delta\)ABC vuông cân tại A. Kẻ tia phân giác của góc A cắt BC tại H. Trên tia AB, AC lấy điểm N và M sao cho BN=AM. Chứng minh rằng:
a, \(\Delta\)AHN=\(\Delta\)CHM
b,\(\Delta\)AHM=\(\Delta\)NHN
c,\(\Delta\)MHN vuông cân
câu này thì em ko biết vì em mới học lớp6
Bài làm
a) Vì tam giác ABC vuông cân ở A
Mà AH là phân giác
=> AH là trung tuyến.
=> AH = BH = HC
=> Tam giác AHC cân tại H
=> AH = HC
=> \(\widehat{HAC}=\widehat{HCA}\)
Mà \(\widehat{HAB}=\widehat{HAC}\)( Do AH phân giác )
=> \(\widehat{HCA}=\widehat{HAB}\)
Ta có: AN + NB = AB
AM + MC = AC
mà AB = AC, BN = AM
=> AN = MC
Xét tam giác AHN và tam giác CHM có:
AN = MC ( cmt )
\(\widehat{HCA}=\widehat{HAB}\)( cmt )
AH = HC ( cmt )
=> Tam giác AHN = tam giác CHM ( c.g.c)
b) Vì tam giác AHN = tam giác CHM ( cmt )
=> NH = HM
Vì AH trung tuyến
=> BH = HC
Xét tam giác AHM và tam giác NHB có:
NH = HM ( cmt )
BN = AM ( gt )
HB = HC ( cmt )
=> Tam giác AHM = tam giác NHB ( c.c.c )
Hình bạn ỉn vẽ sai nhé
Cho Δ ABC vuông cân tại A. Kẻ tia phân giác của góc A cắt BC tại H. Trên tia AB, AC lấy điểm N và M sao cho BN=AM. Chứng minh rằng: a, Δ AHN= Δ CHM b, Δ AHM= Δ BHN c, Δ MHN vuông cân
a: Xet ΔAHN và ΔCHM có
AH=CH
góc HAN=góc HCM
AN=CM
=>ΔAHN=ΔCHM
b: Xet ΔAHM và ΔBHN co
AH=BH
góc HAM=góc HBN
AM=BN
=>ΔAHM=ΔBHN
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).
a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)
b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.
c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.
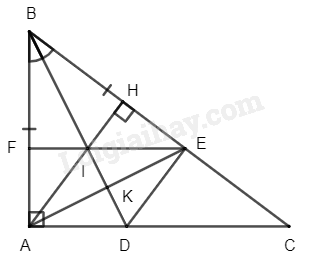
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:
\(BA = BE\) (gt)
\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)
\(BD\) chung
Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)
b) Vì \(\Delta ABD = \Delta EBD\) (cmt)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DE \bot BC\)
Mà \(AH \bot BC\) (gt)
Suy ra \(AH\) // \(DE\)
Suy ra \(ADEH\) là hình thang
Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)
Suy ra \(ADEH\) là hình thang vuông
c)
Gọi \(K\) là giao điểm của \(AE\) và \(AD\)
Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)
Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )
Suy ra \(BK\) cũng là đường cao
Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)
Suy ra \(I\) là trực tâm của \(\Delta ABE\)
Suy ra \(EF \bot AB\)
Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))
Suy ra \(AC\) // \(EF\)
Suy ra \(ACEF\) là hình thang
Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)
Suy ra \(ACEF\) là hình thang vuông
Câu 1. Cho tam giác ABC vuông tại A (AB<AC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AM=AB
a) Chứng minh: DB=DM
b) Gọi E là giao điểm AB và MD. Chứng minh \(\Delta BED=\Delta MCD\)
c) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàng
Câu 2 . Cho \(\Delta ABC\)có AB<AC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BA=BE
a) Chứng minh: DA=DE
b) Tia ED cắt BA tại F. Chứng minh \(\Delta DAF=\Delta DEC\)
c) Gọi H là trung diểm của FC. Chứng minh ba điểm B,D,H thẳng hàng
Câu 3. Cho \(\Delta ABC\)cân tại A. Kẻ AH vuông góc với BC (\(H\in BC\))
a) Chứng minh: HB=HC
b) Kẻ \(HD\perp AB\left(D\in AB\right)\)và \(HE\perp AC\left(E\in AC\right)\). Chứng minh \(\Delta HDE\)cân
Câu 4. Cho tam giác ABC vuông tại B, đường phân giác \(AD\left(D\in BC\right)\). Kẻ DE vuông góc với \(AC\left(E\in AC\right)\)
a) Chứng minh: \(\Delta ABD=\Delta AED;\)
b) BE là đường trung trực của đoạn thẳng AD
c) Gọi F là giao điểm của hai đường thẳng AB và ED Chứng minh BF=EC
Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
Câu 4:
a: Xét ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
góc BAD=góc EAD
Do đó: ΔBAD=ΔEAD
b: Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE
c: Xét ΔBDF vuông tại B và ΔEDC vuông tại E có
DB=DE
góc BDF=góc EDC
Do đó: ΔBDF=ΔEDC
Suy ra: BF=EC
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC tại H. Trên tia đối của tia DH lấy điểm K sao cho DK = DC
a) Chứng minh \(\Delta\)ABD = \(\Delta\)HBD
b) Chứng minh BD là đường trung trực của AH
c) Chứng minh ba điểm B,A,K thẳng hàng
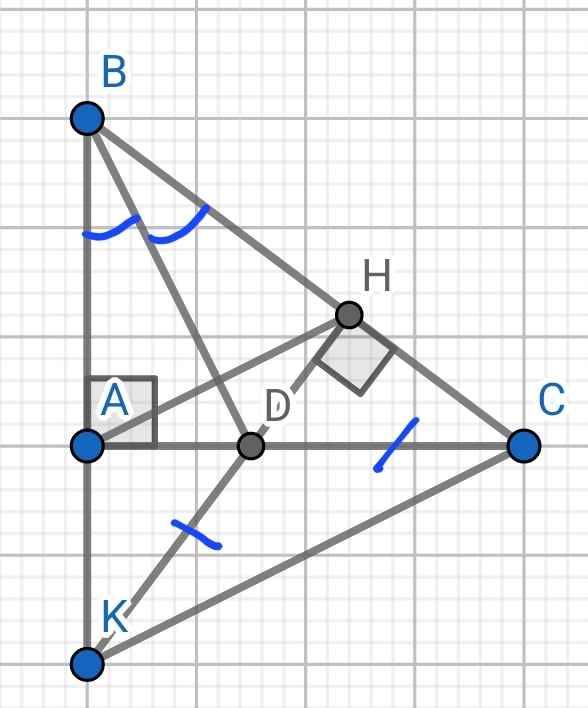
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng
Cho \(\Delta ABC\) cân tại A. Trên cạnh BC lấy điểm D ( D khác B,C ). Trên tia đối của tia CB lấy điểm E sao cho CE=BD. Đường vuông góc với BC kẻ từ D cắt BA tại M. Đường vuông góc với BC kẻ từ E cắt tia AC tại I.
a) Chứng minh rằng: DM=EN
b) Chứng minh rằng: IM=IN; BC<MN
c) Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I. Chứng minh rằng: \(\Delta BMO=\Delta CNO\). Từ đó suy ra điểm O cố định.
Bài 5 : Cho \(\Delta ABC\) có AB = AC , lấy M là trung điểm của BC . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD = CE . Chứng minh :
b )\(\Delta ABD=\Delta ACE\) a ) AM vuông góc với BC
c )\(\Delta ACD=\Delta ABE\) d ) AM là tia phân giác của góc DAE
Bài 6 : Cho tam giác ABC ( AC > AB ) . Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE = AB .
a ) Chứng minh BD = DE
b ) Kéo dài AB và DE cắt nhau tại K. Chứng minh góc AKD bằng góc ACD .
c ) Chứng minh \(\Delta KBE=\Delta CEB\)
d ) Tìm điều kiện của tam giác ABC để DE vuông góc với AC .
Bài 7 Cho tam giác ABC , P là trung điểm của AB . Đường thẳng qua P và song song với BC cắt AC ở đường thẳng qua Q và song song với AB cắt BC ở F. Chứng minh rằng :
a ) AP = QF
b ) \(\Delta APQ=\Delta QFC\)
c ) Q là trung điểm của AC
d ) Lấy điểm I thuộc tia đối của tia QP sao cho QI = QP . Chứng minh CI // AB
Bài 8 : Cho đoạn thẳng AB . Trên hai nửa mặt phẳng đối nhau bờ AB , kẻ tia Ax và By cùng vuông góc với AB . Trên tia Ax , By lần lượt lấy hai điểm C , D sao cho AC = BD .
a ) Chứng minh AD = BC
. b ) Chứng minh AD // BC .
c ) Gọi 0 là trung điểm của AB . Trên BC lấy điểm E , trên AD lấy điểm F sao cho CE = DF . Chứng minh ( là trung điểm của EF .
Mình đang cần gấp ạ
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\); tia phân giác của góc A cắt BC tại M. Trên tia đối của tia MA lấy điểm D sao MD = MA.
a) Chứng minh: \(\Delta ABM=\Delta ACM\)
b) Chứng minh: BC vuông góc với AM.
c) Chứng minh: AB // CD .
d) Cho biết, nếu\(\widehat{ACB}=55^o\), tính số đo\(\widehat{MDC}\) .
a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
Cho tam giác ABC vuông tại A có AB nhỏ hơn AC. Gọi M là trung điểm của cạnh BC. Trên đoạn AM lấy điểm E bất kì khác A và M. Trên tia đối của tia MA lấy điểm F sao cho M là trung điểm của EF
a) Chứng minh \(\Delta BME=\Delta CMF\)
b) Từ C kẻ đường thẳng vuông góc với AC cắt tai AM tại N. Chứng minh góc ABE bằng góc NCF