Cho ABC vuông tại A có đường cao AH và tia phân giác BI.
a) Giả sử AB = 6cm, BC = 10cm. Tính AC và AH
b) Qua C kẻ đường thẳng vuông góc với BI tại D. Gọi E là giao điểm của BA và CD. Chứng
minh rằng EA.EB = EC.ED

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH và tia p/g BI a/Giả sử AB = 6cm, BC = 20cm.Tính AC và AH b/Qua C kẻ đường thẳng vuông góc với BI tại D.Gọi E là giao điểm của BA và CD từ đó suy ra tam giác EAD đồng dạng với tam giác ECB c/ Gọi E là hình chiếu của D trên BE.CMR (BD/DE)^2 = BF/FE d/Gọi O là giao điểm của AD và FC CMR. S OCD = 1/4 S OCA
Chỉ cần làm b và c thôi nha
Gọi O là giao điểm của AD và FC CMR. S OCD = 1/4 S OCA
Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm và đường cao AH a. Cm tam giác ABC ~ tam giác AHB b. Tính BC,HB c. Qua B vẽ đường thẳng d vuông góc với AC, tia phân giác của góc BAC cắt BC tại M và cắt đường thẳng d tại N. Cm AB/AC= MN/AM
a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, phân giác BI. Qua C kẻ đường thẳng vuông góc với BI tại D. Gọi E là giao điểm của AB và CD. Gọi F là hình chiếu của D trên BE. Chứng minh: (BD/DE)^2=BF/EF
Lời giải:
Xét tam giác $BFD$ và $BDE$ có:
$\widehat{B}$ chung
$\widehat{BFD}=\widehat{BDE}=90^0$
$\Rightarrow \triangle BFD\sim \triangle BDE$ (g.g)
$\Rightarrow \frac{BF}{BD}=\frac{BD}{BE}\Rightarrow BD^2=BF.BE(1)$
Tương tự, ta chứng minh được $\triangle EFD\sim \triangle EDB$ (g.g)
$\Rightarrow \frac{EF}{ED}=\frac{ED}{EB}\Rightarrow DE^2=EF.EB(2)$
Từ $(1);(2)\Rightarrow (\frac{BD}{DE})^2=\frac{BF}{EF}$
Ta có đpcm.
Đúng 2
Bình luận (0)
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec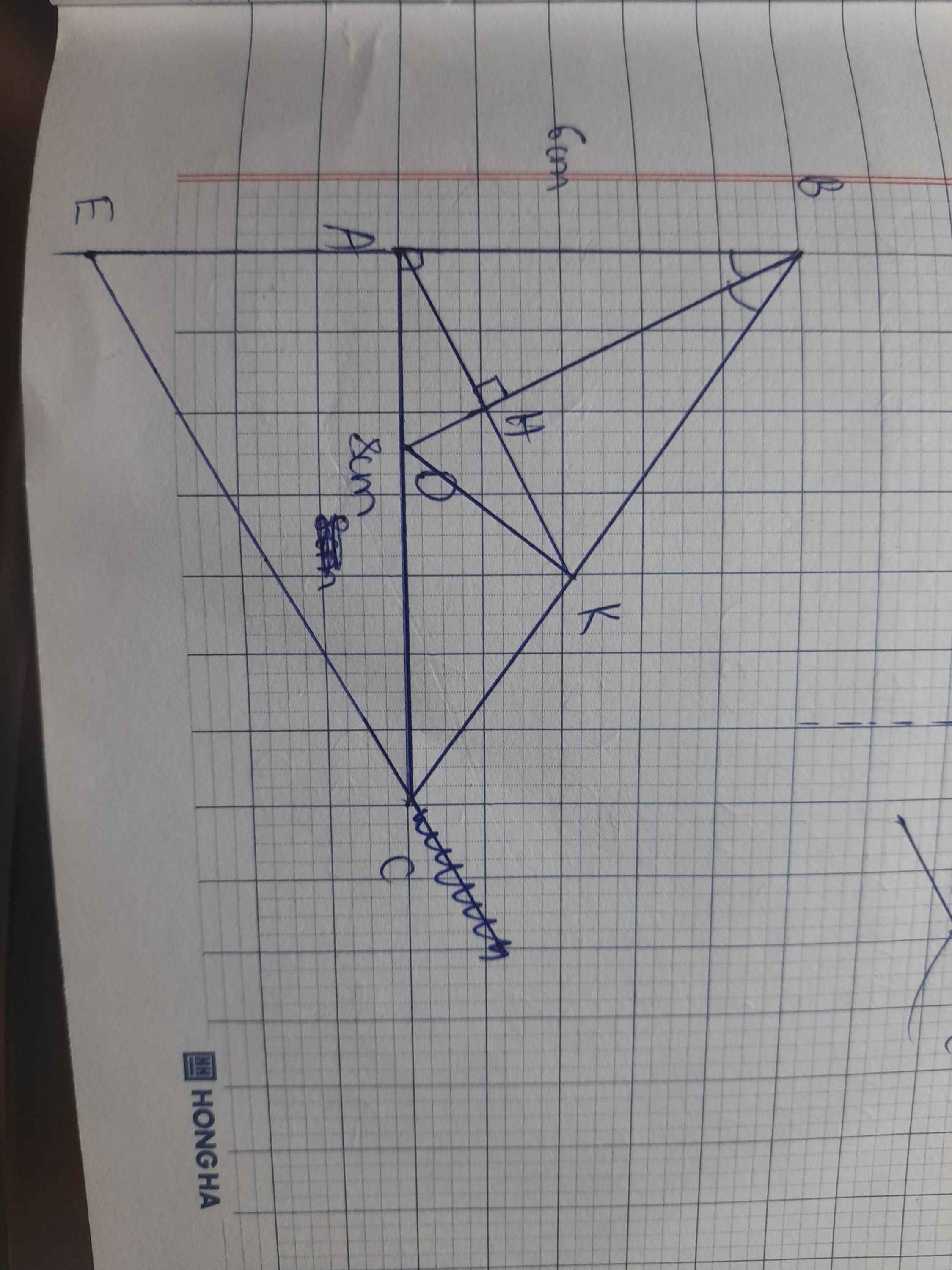
a) Xét tam giác vuông ABC
Theo định lý Py-ta-go ta có :
AB2 + AC2 = BC2
=> 62 + 82 = BC2
=> 36 + 64 = BC2
=> 100 = BC2
=> BC = 10cm
Đúng 1
Bình luận (0)
Bài 3: Cho ∆ ABC vuông tại A, đường phân giác BE, kẻ EH vuông góc với BC tại H, gọi K là giao điểm của 2 đường thẳng BA và HE.
a) Chứng minh rằng AE=HE, AB=BH.
b) Biết AB=6cm, BC=10cm. Tính độ dài AC, BK.
c) Chứng minh rằng AH//KC.
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: EA=EH và BA=BH
b: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: AK=HC
Xét ΔBKC có BA/AK=BH/HC
nên AH//KC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường phân giác BD, kẻ DE vuông góc với BC tại E, gọi H là giao điểm của hai đường thẳng BA và ED. a) Chứng minh rằng AD = DE, AB = BE. b) Biết AB = 6cm, BC = 10cm. Tính độ dài AC, BH. c) Chứng minh rằng AE // HC.
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: BA=BE và DA=DE
b: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
c: Xét ΔADH vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADH}=\widehat{EDC}\)
Do đó: ΔADH=ΔEDC
Suy ra: AH=EC
Xét ΔBHC có BA/AH=BE/EC
nên AE//HC
Đúng 1
Bình luận (1)
Bài 1: Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt đường thẳng AB, AC tại E và D
a) Tính AM ?
b) Tam giác BEC cân
Bài 2: Cho tam giác ABC vuông tại A, phân giác BE, kẻ EH vuông góc với BC ( H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh BE là đường trung trực của AH.
Bài 1: Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt đường thẳng AB, AC tại E và D
a) Tính AM ?
b) Tam giác BEC cân
Bài 2: Cho tam giác ABC vuông tại A, phân giác BE, kẻ EH vuông góc với BC ( H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh BE là đường trung trực của AH.
Bài 1: Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt đường thẳng AB, AC tại E và D
a) Tính AM ?
b) Tam giác BEC cân
Bài 2: Cho tam giác ABC vuông tại A, phân giác BE, kẻ EH vuông góc với BC ( H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh BE là đường trung trực của AH.

















