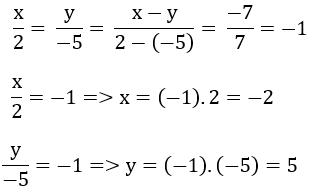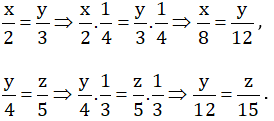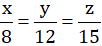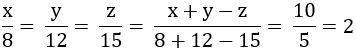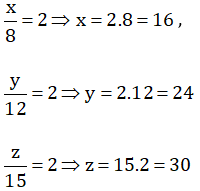Tìm x,y biết x(x-y)=3 phần 10 và y(x-y)=-3 phần 50

Những câu hỏi liên quan
Tìm x,y,z biết x-1 phần 2 = y-2 phần 3 = y-3 phần 4 và 2x + 3y = 50
Tìm x,y,z biết x-1 phần 2 = y-2 phần 3 = y-3 phần 4 và 2x + 3y = 50
Tìm x,y,z biết x-1 phần 2 = y-2 phần 3 = y-3 phần 4 và 2x + 3y = 50
tìm x y z biết x phần 10 = y phần 5 , y phần 2 = z phần 3 và x + 4z =320
\(\dfrac{x}{10}\) = \(\dfrac{y}{5}\) ⇒ \(x\) = \(\dfrac{y}{5}\) \(\times\) 10 = 2y
\(\dfrac{y}{2}\) = \(\dfrac{z}{3}\) = ⇒ \(\dfrac{4y}{8}\) = \(\dfrac{4z}{12}\) ⇒ 4z = \(\dfrac{4y}{8}\) \(\times\) 12 = 6y
Theo bài rat ta có:
\(x+4z\) = 2y + 6y = 320 ⇒ 8y = 320 ⇒ y = 320: 8 =40
\(x\) = 40 \(\times\) 2 = 80
z = \(\dfrac{y}{2}\) \(\times\) 3 = \(\dfrac{40}{2}\) \(\times\) 3 = 60
Vậy \(x\) = 80; y = 40; z = 60
Đúng 0
Bình luận (0)
tìm 3 số x , y , z biết x phần 2 = y phần 3 ; y phần 4 = z phần 5 và x+y-z =10
từ \(\frac{x}{2}\)=\(\frac{y}{3}\)=>\(\frac{x}{8}\)=\(\frac{y}{12}\)
\(\frac{y}{4}\)=\(\frac{z}{5}\)=>\(\frac{y}{12}\)=\(\frac{z}{15}\)
=>\(\frac{x}{8}\)=\(\frac{y}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
\(=>\hept{\begin{cases}x=2.8=16\\y=2.12=24\end{cases}z=2.15=30}\)
Đúng 0
Bình luận (0)
Câu 1:Tìm x,y :
a,x+1 phần 2=0,5 phần 1,2
b,x/5=y/-7 và x+y=10
c,(x+1 mũ 3)=-8 phần 27
Câu 2:Tìm x,y biết:
a,x phần y =4 phần -9 và x-y=26
b, 2x=5y và 3x-y=1
c,|2x-9|-1 phần 2=-2 phần 5
Câu 3
a, Tính góc ở đỉnh của 1 tam giác cân biết góc ở đáy là 50 độ
b,3x phần 5=2y phần -9 và x-y =1
Ai giải dc thì giúp m ,m sẽ kích nha!!
tìm ba số x,y,z biết rằng: xphần 2=y phần 3, y phần 4 = z phần 5 và x+y-z=10
\(\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\)
=> \(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\) (x+y-z=10)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
\(\hept{\begin{cases}\frac{x}{8}=2\Rightarrow x=2.8=16\\\frac{y}{12}=2\Rightarrow y=2.12=24\\\frac{z}{15}=2\Rightarrow z=2.15=30\end{cases}}\)
Vậy x=16 ; y=24 và z=30
Đúng 0
Bình luận (0)
tìm x,y,z biết x+y+z khác 0 và x phần y+z-3= y phần x+z= z phần x+y+3= 1 phần 4044 x+y+z
\(\dfrac{x}{y+z-3}=\dfrac{y}{x+z}=\dfrac{z}{x+y+3}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=\dfrac{1}{4044\left(x+y+z\right)}\)
\(\Rightarrow\left\{{}\begin{matrix}y+z-3=2x\\x+z=2y\\x+y+3=2z\end{matrix}\right.\) và \(4044\left(x+y+z\right)=2\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=3x+3\\x+y+z=3y\\x+y+z=3z-3\end{matrix}\right.\\ \Rightarrow3x+3=3y=3z-3\\ \Rightarrow x+1=y=z-1\)
\(\left\{{}\begin{matrix}x=y-1\\z=y+1\end{matrix}\right.\)
Lại có \(4044\left(x+y+z\right)=2\)
\(\Rightarrow4044\left(y-1+y+y+1\right)=2\\ \Rightarrow4044\cdot3y=2\\ \Rightarrow y=\dfrac{1}{674}\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{673}{674}\\z=\dfrac{675}{674}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a) tìm hai số x và y biết x:2 = y: (-5) và x-y =-7
b) tìm ba số x,y,z biết x phần 2 = y phần 3 ,y phần 4 và z phần 5 và x+y-z=10
cảm ơn trước ak
a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
Đúng 2
Bình luận (0)
b)
Do đó ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Đúng 0
Bình luận (0)