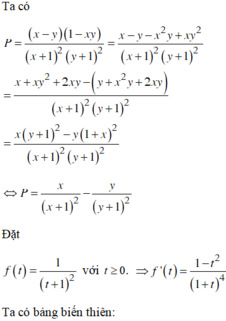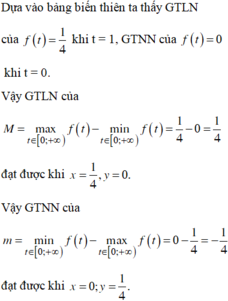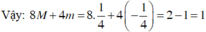Cho 2 số không âm x,y sao cho x+y=a=const (a là hằng số có giá trị không đổi). Tìm Giá trị lớn nhất của P=40x+xy

Những câu hỏi liên quan
Cho 2 số không âm x,y sao cho x+y=R=const. Tìm Giá trị lớn nhất của P=40x+xy theo R
giúp mình gấp với ạ mình cảm ơn nhiều!
1 cho tam giác ABC nội tiếp đường trong tâm O, đường cao AH,BF,CE, kẻ HE vương góc AB,HF vuông góc AC,HE giao BF tại M,HF giao CE tại N.chứng minh MN song song BC, 2 Tam giác ABC nội tiếp trong (O). Đường thẳng xy là tiếp tuyến với đường tròn tại A của (O). Đường thẳng song song với BC cắt cạnh AB tại D và cạnh AC tại E.Chứng minh BCED nội tiếp.3 Cho 2 số không âm x,y sao cho x+yaconst (a là hằng số có giá trị không đổi). Tìm Giá trị lớn nhất của P40x+xy
Đọc tiếp
1 cho tam giác ABC nội tiếp đường trong tâm O, đường cao AH,BF,CE, kẻ HE vương góc AB,HF vuông góc AC,HE giao BF tại M,HF giao CE tại N.chứng minh MN song song BC,
2 Tam giác ABC nội tiếp trong (O). Đường thẳng xy là tiếp tuyến với đường tròn tại A của (O). Đường thẳng song song với BC cắt cạnh AB tại D và cạnh AC tại E.Chứng minh BCED nội tiếp.
3 Cho 2 số không âm x,y sao cho x+y=a=const (a là hằng số có giá trị không đổi). Tìm Giá trị lớn nhất của P=40x+xy
Cho 2 số không âm x,y sao cho x+y=a=const (a là hằng số có giá trị không đổi). Tìm Giá trị lớn nhất của P=40x+xy
giúp mình gấp với ạ mình cảm ơn nhiều!
Lời giải:
Thay $y=a-x$ vào biểu thức $P$. Vì $x+y=a; x,y\geq 0$ nên $a\geq 0; 0\leq x,y\leq a$
Ta có:$P=40x+x(a-x)=-x^2+(40+a)x$
Nếu $a\geq 40$:
$P=-[x^2-(40+a)x]=(\frac{40+a}{2})^2-[x^2-2.x.\frac{40+a}{2}+(\frac{40+a}{2})^2]=(\frac{40+a}{2})^2-(x-\frac{40+a}{2})^2$
Dễ thấy $(x-\frac{40+a}{2})^2\geq 0$ với mọi $a\leq x\geq 0$
Do đó: $P\leq \left(\frac{40+a}{2})^2$ hay $P_{\max}=\left(\frac{40+a}{2}\right)^2$
Giá trị này đạt đc khi $x=\frac{40+a}{2}, b=\frac{a-40}{2}$
Nếu $a< 40$:
$P=-x^2+(40+a)x=40x-ax+a^2-(x-a)^2$=x(40-a)+a^2-(x-a)^2$
Vì $a< 40; x\leq a\Rightarrow x(40-a)\leq a(40-a)$
$(x-a)^2\geq 0$ với mọi $0\leq x\leq a$. Do đó: $P\leq a(40-a)+a^2=40a$
Vậy $P_{\max}=40a$ khi $x=a; y=0$
Lời giải:
Thay $y=a-x$ vào biểu thức $P$. Vì $x+y=a; x,y\geq 0$ nên $a\geq 0; 0\leq x,y\leq a$
Ta có:$P=40x+x(a-x)=-x^2+(40+a)x$
Nếu $a\geq 40$:
$P=-[x^2-(40+a)x]=(\frac{40+a}{2})^2-[x^2-2.x.\frac{40+a}{2}+(\frac{40+a}{2})^2]=(\frac{40+a}{2})^2-(x-\frac{40+a}{2})^2$
Dễ thấy $(x-\frac{40+a}{2})^2\geq 0$ với mọi $0\leq x\leq a$
Do đó: $P\leq \left(\frac{40+a}{2}\right)^2$ hay $P_{\max}=\left(\frac{40+a}{2}\right)^2$
Giá trị này đạt đc khi $x=\frac{40+a}{2}, b=\frac{a-40}{2}$
Nếu $a< 40$:
$P=-x^2+(40+a)x=40x-ax+a^2-(x-a)^2a=x(40-a)+a^2-(x-a)^2$
Vì $a< 40; x\leq a\Rightarrow x(40-a)\leq a(40-a)$
$(x-a)^2\geq 0$ với mọi $0\leq x\leq a$. Do đó: $P\leq a(40-a)+a^2=40a$
Vậy $P_{\max}=40a$ khi $x=a; y=0$
Cho x, y, z là các số không âm và x+y+z=1. Tìm giá trị lớn nhất của M với M= xy+yz+zx
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn ^{x^2+y^2+z^2le xyz}Hãy tìm giá trị lớn nhất của biểu thức Afrac{x}{x^2+yz}+frac{y}{y^2+zx}+frac{z}{z^2+xy}2. Cho x,y,z là các số thực không âm thỏa mãn x^2+y^2+z^23Tìm giá trị lớn nhất của biểu thức Bxy+yz+zx+frac{5}{x+y+z}
Đọc tiếp
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn \(^{x^2+y^2+z^2\le xyz}\)
Hãy tìm giá trị lớn nhất của biểu thức \(A=\frac{x}{x^2+yz}+\frac{y}{y^2+zx}+\frac{z}{z^2+xy}\)
2. Cho x,y,z là các số thực không âm thỏa mãn \(x^2+y^2+z^2=3\)
Tìm giá trị lớn nhất của biểu thức \(B=xy+yz+zx+\frac{5}{x+y+z}\)
Cho x, y là hai số thực không âm thay đổi.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức  \(\frac{\left(x-y\right)\left(1-xy\right)}{\left(1+x\right)^2\left(1+y\right)^2}\)
\(\frac{\left(x-y\right)\left(1-xy\right)}{\left(1+x\right)^2\left(1+y\right)^2}\)
Cho các số thực không âm x,y thay đổi. M, n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P
x
-
y
1
-
x
y
x
+
1...
Đọc tiếp
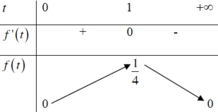
Cho các số thực không âm x,y thay đổi. M, n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x - y 1 - x y x + 1 2 y + 1 2 . Giá trị của 8M + 4m bằng:
A. 3.
B. 1.
C. 2.
D. 0.
Cho x và y là hai số thực không âm thỏa mãn x + y = 4 . Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = \(x^4+y^4-4xy+3\)
\(P=\left(x^2+y^2\right)^2-2x^2y^2-4xy+3=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2-4xy+3\)
\(=\left(16-2xy\right)^2-2x^2y^2-4xy+3=2x^2y^2-68xy+259\)
\(4=x+y\ge2\sqrt[]{xy}\Rightarrow0\le xy\le4\)
Đặt \(xy=a\Rightarrow0\le a\le4\)
\(P=2a^2-68a+259=259-2a\left(34-a\right)\le259\)
\(P_{max}=259\) khi \(a=0\) hay \(\left(x;y\right)=\left(4;0\right);\left(0;4\right)\)
\(P=\left(2a^2-68a+240\right)+19=2\left(4-a\right)\left(30-a\right)+19\ge19\)
\(P_{min}=19\) khi \(a=4\) hay \(x=y=2\)
Đúng 1
Bình luận (0)
Cho x, y, z là các số thực không âm thỏa mãn \(x^2+y^2+z^2=4\). Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P=x+y+z
Ta có :
\(\left(1^2+1^2+1^2\right)\left(x^2+y^2+z^2\right)\ge\left(1.x+1.y+1.z\right)^2\) (Bunhia)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow\left(x+y+z\right)^2\le3.4=12\)
\(\Rightarrow-2\sqrt{3}\le x+y+z\le2\sqrt{3}\)
Đúng 0
Bình luận (0)
Bạn trên làm sai r. X+y+z ko âm cơ mà sao lại có gtnn là -2√3??
Đúng 0
Bình luận (0)