Hàm số y = -23-23x nhận giá trị dương khi :
A. x<0
B. x>0
C. x=0
D. Không xác định
Những câu hỏi liên quan
Hàm số y = − 2 3 x nhận giá trị dương khi
A. x < 0
B. x > 0
C. x = 0
D. Không xác định được
Do − 2 3 < 0 nên để y = − 2 3 x nhận giá trị dương thì x < 0
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng 1
c. Nhận giá trị dương
d. Nhận giá trị âm
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
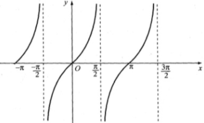
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
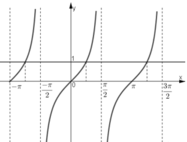
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
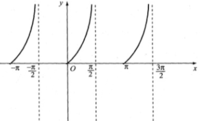
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
Đúng 0
Bình luận (0)
24 tháng 11 2021 lúc 17:47
cho hàm số y = -2 x
a , hãy xác định giá trị của biến x khi hàm số nhận giá trị bằng ( -4 )
b, tìm giá trị của hàm số với x = -1
c, vẽ đồ thị hàm số trên
mình cần gấp
Xác định parabol (P): y a
x
2
+ bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng
3
4
khi x
1
2
và nhận giá trị bằng 1 khi x 1. A. y −
x
2
+ x + 1 B. y
x
2
+ x – 1 C. y
x
2
- x + 2 D. y...
Đọc tiếp
Xác định parabol (P): y = a x 2 + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng 3 4 khi x= 1 2 và nhận giá trị bằng 1 khi x = 1.
A. y = − x 2 + x + 1
B. y = x 2 + x – 1
C. y = x 2 - x + 2
D. y = x 2 - x + 1
a) Cho hàm số
y
f
(
x
)
2
3
x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)b) Cho hàm số
y
g
(
x
)
2
3
x
+
3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
Đọc tiếp
a) Cho hàm số
y = f ( x ) = 2 3 x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)
b) Cho hàm số
y = g ( x ) = 2 3 x + 3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
a) Ta có:
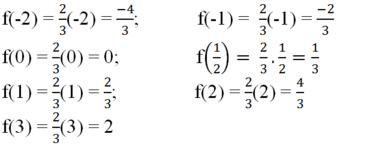
b) Ta có:
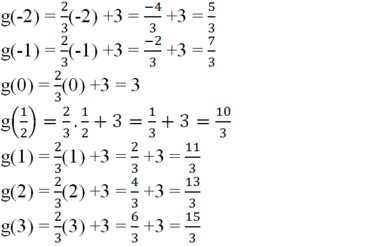
c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Hai hàm số
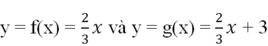
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
Đúng 0
Bình luận (0)
Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 11:43
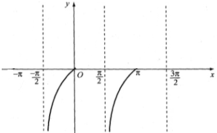
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−π2;2π] để hàm số y=cotx nhận giá trị dương.
cot x>0
=>\(x\in\left(0;\dfrac{pi}{2}\right)\cup\left(pi;\dfrac{3}{2}pi\right)\)
Đúng 0
Bình luận (0)
Xác định các hệ số a b c để hàm số y=ax2+bx+c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng 1 khi x =1
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.
Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)
Đúng 0
Bình luận (0)
Xác định parabol (P) ; y ax2+bx+ c biết: Hàm số y ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x1/2 và nhận giá trị bằng khi x1. A. y x2+ x+1. B. y- x2-x+1. C. y -x2-x-1. D. y x2-x+1
Đọc tiếp
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
A. y= x2+ x+1.
B. y=- x2-x+1.
C. y= -x2-x-1.
D. y= x2-x+1
