a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>HB=HC và \(\widehat{BAH}=\widehat{CAH}\)

b: Ta có: HB=HC

H nằm giữa B và C

Do đó: H là trung điểm của BC

=>\(HB=HC=\dfrac{BC}{2}=4\left(cm\right)\)

ΔAHB vuông tại H

=>\(AH^2+HB^2=AB^2\)

=>\(AH^2=5^2-4^2=9\)

=>\(AH=\sqrt{9}=3\left(cm\right)\)

c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có

AH chung

\(\widehat{DAH}=\widehat{EAH}\)

Do đó: ΔADH=ΔAEH

=>HD=HE

=>ΔHDE cân tại H

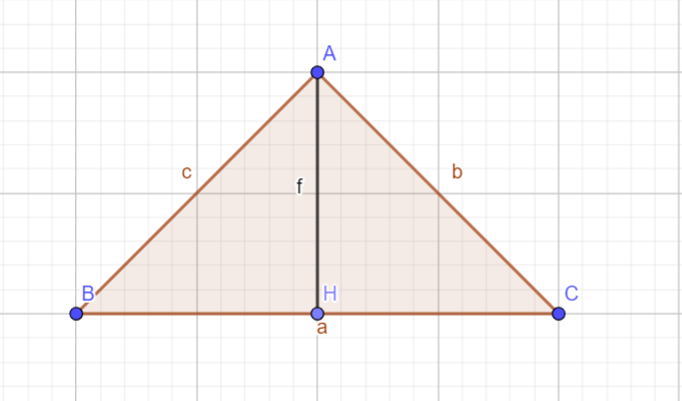
a) Xét tam giác AHB và AHC có:

AC = BC (gt)

\(\widehat{AHB}=\widehat{AHC}\) (AH vuông góc BC)

=> AHB = AHC (ch-gv)

=> HB = HC (cạnh tương ứng)

\(\widehat{BAH}=\widehat{CAH}\) (góc tương ứng)

b) Ta có HB =  HC (cmt)

Mặt khác AH là cạnh góc vuông của tam giác vuông AHC

Áp dụng định lý Pitago ta có:

\(AC^2=AH^2+HC^2\\ =>10^2=AH^2+6^2\\ =>100=AH^2+36\)

\(=>AH^2=100-36=64\\ =>AH=\sqrt{64}=8\)

:
a)Vì △ABC cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
 HB=HC và BAHˆ=CAHˆ
b)HC=BC2=82=4
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
AH2=AC2−HC2=.......
 AH=...........
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
Bˆ=Cˆ(△ABC cân)
Do đó: △BDH=△CEH
 DH =EH 
 dpcm

Bài 3 :
a)Vì △ABC cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
 HB=HC và BAHˆ=CAHˆ
b)HC=BC2=82=4
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
AH2=AC2−HC2=.......
 AH=...........
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
Bˆ=Cˆ(△ABC cân)
Do đó: △BDH=△CEH
 DH =EH 
 dpcm

a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC

b.áp dụng định lý pitago ta có:

\(AB^2=AH^2+HB^2\)

\(5^2=AH^2+\left(8:2\right)^2\)

\(AH=\sqrt{5^2-4^2}=3cm\)

c.Xét tam giác vuông BHD và tam giác vuông CHE, có:

BH = CH ( cmt )

góc B = góc C ( ABC cân )

Vậy tam giác vuông BHD = tam giác vuông CHE 

=> HD = HE 

=> HDE cân tại H

d.ta có AB = AD + DB

           AC = AE + EC

Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )

=> AD = AE 

=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )

Chúc bạn học tốt !!!!

a, Xét \(\Delta ABH\) và\(\Delta ACH\) CÓ:

\(AHchung\)

AB = AC 

\(\widehat{AHB}=\widehat{AHC}\)

\(\Rightarrow\Delta ABH=\Delta ACH\)(cạnh huyền cạnh góc vuông)

=> BH = HC ( 2 cạnh tương ứng )

b,Do BC = 8cm => BH = 4cm 

Áp dụng định lý Py ta go vào tam giác vuông ABH có :

\(AH^2+BH^2=AB^2\)

\(\Rightarrow AH^2=AB^2-BH^2\)\(\Rightarrow AH^2=5^2-4^2=25-16=9\)\(\Rightarrow AH=3\left(cm\right)\)

c,\(Xét\Delta DBH\) và\(\Delta ECH\) có :

\(\widehat{ABH}=\widehat{ACH}\)

BH = HC

\(\widehat{BDH}=\widehat{CEH}\)

\(\Rightarrow\Delta DBH=\Delta ECH\)\(\Rightarrow DH=EH\)=> \(\Delta DHE\) cân tại H

cho mình 1 tym nha

a: Ta có: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC và AH là tia phân giác của góc BAC

=>HB=HC và góc BAH=góc CAH

b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có 
AH chung

\(\widehat{DAH}=\widehat{EAH}\)

Do đó: ΔADH=ΔAEH

Suy ra: AD=AE và HD=HE

hay ΔHED cân tại H

tam giác AHB vuông tại BH=> AH^2 + HB^2 = AB^2 (pytago)

AH = 12; BH = 9 

=> AB^2 = 9^2 + 12^2 = 225

=> AB = 15 do AB> 0 => AB^2 = 225    (1)

tương tự chứng minh được AC = 20 => AC^2 = 400    (2)

có CH + HB = BC  

ch = 16; hb = 9

=> BC = 25 => BC^2 = 625   (3)

(1)(2)(3) => Tam giác ABC vuông tại A 

=> góc BAC = 90 

+Kẻ AH vuông góc với BC,tam giác AHC và AHB là tam giác vuông.

áp dụng định lý Pi-ta-go,ta tính cạnh huyền hai tam giác

cạnh huyền tam giác AHB là:

     \(\sqrt{AH^2+HB^2}\)\(=\sqrt{12^2+9^2}=15\)

cạnh huyền tam giác AHC là

     \(\sqrt{AH^2+HC^2}=\)\(\sqrt{12^2+16^2}=20\)

Để góc BAC=90 độ,tam giác đó phải là tam giác vuông.

cạnh huyền tam giác ABC là

     \(\sqrt{20^2+15^2}=25\) ( thỏa mãn )

Vậy \(\widehat{BAC}=\)90 độ

AC^2=AH^2+HC^2(py ta go)

AC^2=144+256=200 cm

suy ra AC=20 cm

AB^2=AH^2+BH^2

BH^2=AB^2-AH^2

BH^2=1169-144=25cm

BH=5cm

Mà BH+HC=BC suy ra 5+16=21

vạy AC=20 cm, BC=21cm

AC = 20

BC = 21

k cho mk nha

a: Ta có: ΔABC cân tại A

mà AH là đường phân giác

nên H là trung điểm của BC

hay BH=CH

b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có 

AH chung

\(\widehat{DAH}=\widehat{EAH}\)

Do đó: ΔADH=ΔAEH

Suy ra: HD=HE

hay ΔHDE cân tại H

c: Xét ΔABC có 

AD/AB=AE/AC

Do đó: DE//BC