Cho tam giác ABC có AB>AC.Kẻ tia phân giác AD(d thuộc BC).Trên cạnh AC lấy điểm E sao cho AE=AB.trên tia AB lấy điểm F sao cho AF=AC.Chứng minh rằng:
a)DB=DE
b)Tam giác BDF=Tam giác EDC
c)F, D, E thẳng hàng
cho tam giác ABC có AB<AC.kẻ tia phân giác AD của BAC(D thuộc BC).trên cạnh AC lấy điểm E sao cho AE=AB.trên tia AB lấy điểm F sao cho À=AC.chứng minh:a, tam giác BDF- tam giác EDC b, BF=EC c, AD vuông góc FC . CÓ VẼ HÌNH.
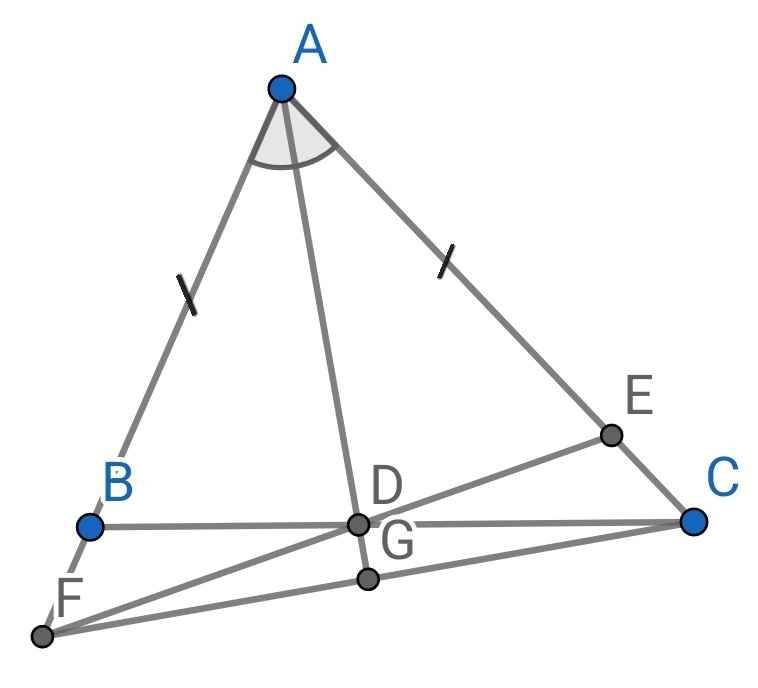 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠EAD
Xét ∆ABD và ∆AED có:
AD là cạnh chung
∠BAD = ∠EAD (cmt)
AB = AE (gt)
⇒ ∆ABD = ∆AED (c-g-c)
⇒ BD = ED (hai cạnh tương ứng)
Do ∆ABD = ∆AED (cmt)
⇒ ∠ABD = ∠AED (hai góc tương ứng)
Ta có:
∠ABD + ∠FBD = 180⁰ (kề bù)
∠AED + ∠CED = 180⁰ (kề bù)
Mà ∠ABD = ∠AED (cmt)
⇒ ∠FBD = ∠CED
Xét ∆BDF và ∆EDC có:
BD = ED (cmt)
∠FBD = ∠CED (cmt)
∠BDF = ∠EDC (đối đỉnh)
⇒ ∆BDF = ∆EDC (g-c-g)
b) Do ∆BDF = ∆EDC (cmt)
⇒ BF = EC (hai cạnh tương ứng)
c) Gọi G là giao điểm của AD và CF
AG là tia phân giác của ∠FAC
⇒ ∠FAG = ∠CAG
Xét ∆AFG và ∆ACG có:
AF = AC (gt)
∠FAG = ∠CAG (cmt)
AG là cạnh chung
⇒ ∆AFG = ∆ACG (c-c-c)
⇒ ∠AGF = ∠AGC (hai góc tương ứng)
Mà ∠AGF + ∠AGC = 180⁰ (kề bù)
⇒ ∠AGF = ∠AGC = 180⁰ : 2 = 90⁰
⇒ AG FC
Hay AD ⊥ FC
1.Cho tam giác ABC có AB=AC . Kẻ tia phân giác AD của góc BAC (D thuộc BC).Trên cạnh AC lấy điểm E sao cho AE=AB, trên tia AB lấy điểm F sao cho AF=AC.Chứng minh rằng:
a)Tam giác ABE=Tam giác ACE
b)AE là đường trung trực của đoạn thẳng BC
2.Cho tam giác ABC có AB<AC .Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB, trên tia AB lấy điểm F sao cho AF=AC. Chứng minh rằng :
a)Tam giác ADF=Tam giác ACD
b)Tam giác BDF=Tam giác EDC
c)BF=AC
d)AD vuông góc FC
Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC
Cho tam giác ABC có AB<AC.KẺ tia phân giác AD của góc BAC (D thuộc BC).Trên cạnh AC lấy điểm E sao cho AE=AB,trên tia AB lấy điểm F sao cho AF=AC.CHúng minh rằng:
a.tam giác ABD=tam giác AED
b.AD vuông góc với FC
c.tam giác BDF=tam giác EDC và BF=EC
d.F,D,E thẳng hàng
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Cho tam giác ABC có AB < AC. Kẻ tia phân giác AD của B A C ^ (D thuộc BC). Trên cạnh AC lấy điểrn E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC, Chứng minh:
a) ∆ B D F = ∆ E D C
b) BF = EC
c) A D ⊥ F C .
cho tam giác ABC có AB < AC. kẻ tia phân giác AD của góc BAC ( D thuộc BC). trên cạnh AC lấy điểm E sao cho AE =AB, trên tia AB lấy điểm F sao cho AF = AC. chứng minh rằng:
a) tam giác BDF = tam giác EDC
b) BF = EC
c) F, D, E thẳng hàng
d) AD vuông góc với FC
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{DBF}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{DEC}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{DBF}=\widehat{DEC}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
b: Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
c: Ta có: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{EDB}=180^0\)
nên \(\widehat{BDF}+\widehat{EDB}=180^0\)
=>E,D,F thẳng hàng
d: ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của FC(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF
Cho tam giác ABC có AB<AC. Kẻ tia phân giác AD của góc BAC, D thuộc BC. Trên cạnh AC,lấy điểm E sao cho AE=AB. Trên tia AB lấy điểm F sao cho AF=AC. Chứng minh
a, tam giác BDF=tam giác EDC
b,BF=EC
c, F,D,E thẳng hàng
d, AD vuông góc với EC
mới gần 10 năm thôi nhỉ tầm giờ chắc chủ câu này có gđ luôn r=)
Cho tam giác ABC nhọn có AB<AC.Kể tia phân giác AD của góc BAC ( D thuộc BC).Trên cạnh AC lấy điểm E sao cho AE =AB, trên tia AB lấy điểm F sao cho AF=AC
A) Chứng minh tam giác BDF= tam giác EDC.
B)Chứng minh ba điểm F,D,E thẳng hàng
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC
Cho tam giác ABC có AB < AC. Kẻ tia phân giác AD của góc BAC ( D thuộc BC ). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a) Tam giác BDF = Tam giác EDC
b) BF = EC
c) F, D, E thẳng hàng
d) AD vuông góc với FC
CÁC BẠN GIÚP MÌNH NHÉ! CẢM ƠN RẤT NHIỀU!
Cho tam giác ABC có AB < AC. Kẻ tia phân giác AD của góc BAC ( D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB, trên tia AB lấy điểm F sao cho AF= AC. Chứng minh rằng:
a.Tam giác BDF = tam giác EDC
b.BF=EC
c.F,D,E thẳng hàng
d.AD vuông góc FC