CAN GAP GAP
GAP

Những câu hỏi liên quan
1. What is gender pay gap?
2. Give some specific examples of gender pay gap in your country.
3. What are the causes of gender pay gap?
4. What are some possible solutions to gender pay gap?
5. What can women do to deal with gender pay gap?
6. What can the government do to close gender pay gap?
7. Give some examples of what governments in the world do to fight gender pay gap?
8. What are some possible solutions from businesses?
9. What can schools do to contribute to solving this problem?
10. Giv...
Đọc tiếp
1. What is gender pay gap?
2. Give some specific examples of gender pay gap in your country.
3. What are the causes of gender pay gap?
4. What are some possible solutions to gender pay gap?
5. What can women do to deal with gender pay gap?
6. What can the government do to close gender pay gap?
7. Give some examples of what governments in the world do to fight gender pay gap?
8. What are some possible solutions from businesses?
9. What can schools do to contribute to solving this problem?
10. Give some specific examples of gender pay gap in the US.
hai so co tong bang 24 va thuong la 0,75 .tim hai so do
nhanh mik can gap gap gap
tuoi bo gap 3 lan tuoi Nam sau 15 nam nua tuoi bo gap doi tuoi Nam tinh tuoi Nam hien nay
giai nhanh nha mik dang can gap
Can gap 
Lời giải:
$Q=\frac{80}{81}a^2+\frac{a^2}{81}+\frac{1}{3a}+\frac{1}{3a}$
$\geq \frac{80}{81}a^2+3\sqrt[3]{\frac{a^2}{81}.\frac{1}{3a}.\frac{1}{3a}}$
$\geq \frac{80}{81}.3^2+\frac{1}{3}=\frac{83}{9}$
Vậy $Q_{\min}=\frac{83}{9}$.
Giá trị này đạt tại $a=3$
Đúng 0
Bình luận (0)
can gap 
8 + 8 =16
16 + 14 = 30
30+14 =44
câu này chx có quy luật rõ ràng lắm bn nhé
Đúng 0
Bình luận (0)
Mot hinh chu nhat co chu vi gap 8 lan chieu rong . Hoi chieu dai gap may lan chieu rong ?
giai giup minh nha chieu nay minh can gap
Goi chiều dài và chiều rong là a,b
Ta có2x(a+b)=8xb
<=>a+b=4xb
<=>a=3xb
<=>chiều dài gẩp 3 lần chiều rộng
Đúng 0
Bình luận (0)
Chu vi gấp lần chiều rộng
=> Tổng chiều dài và rộng (nửa chu vi) gấp 4 lần chiều rộng
=> Chiều dài gấp 3 lần chiều rộng
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. What is a generation gap?
2. Is there a generation gap in your family?
3. In what way can you bridge the gap between family menbers?
4. Do you often run into conflicts with your parents?
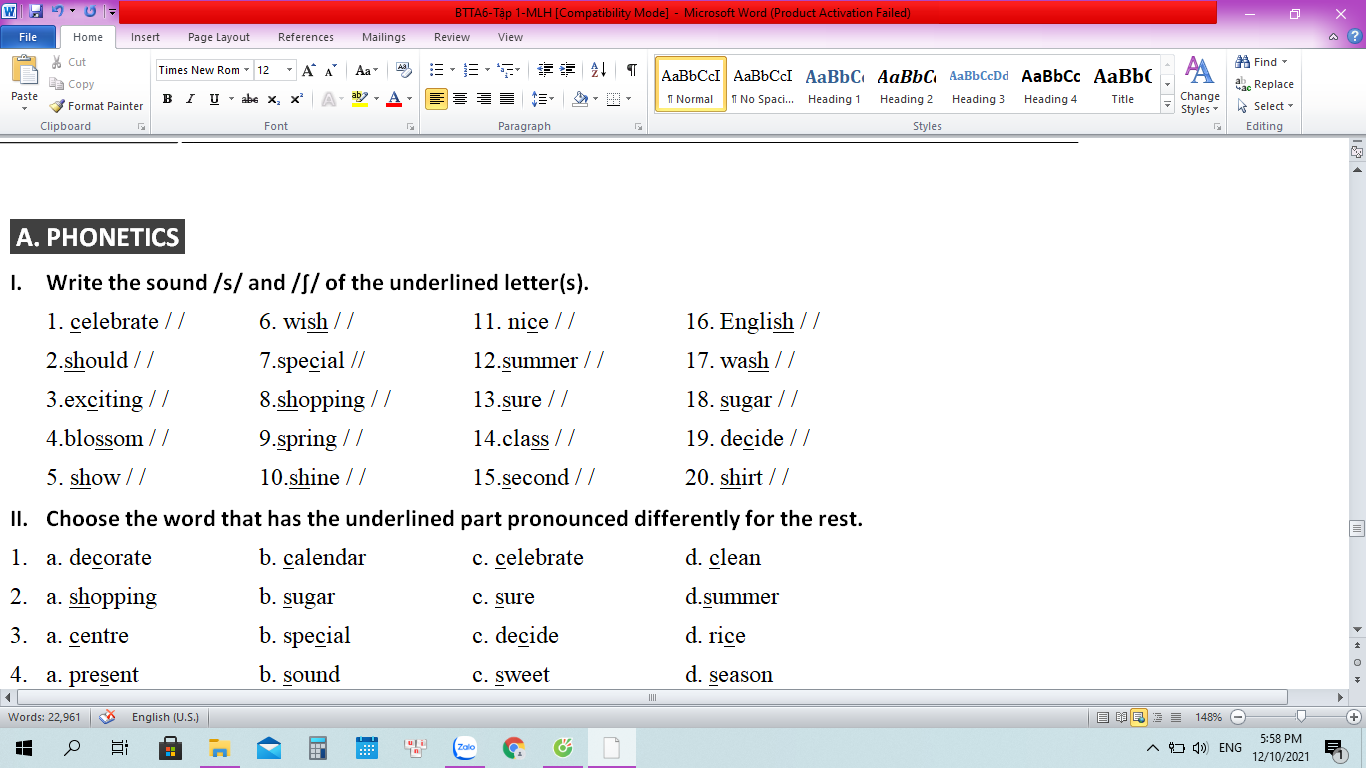 em can gap
em can gap
em can gap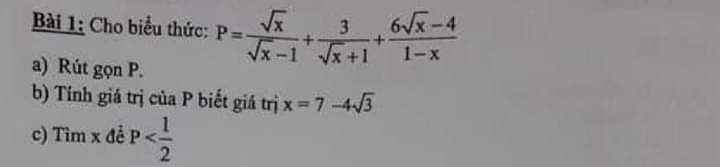
a)Đk \(x\ge0,x\ne1\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
Đúng 1
Bình luận (0)
b)\(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\Rightarrow\sqrt{x}=2-\sqrt{3}\)
\(\Rightarrow P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2-\sqrt{3}-1}{2-\sqrt{3}+1}=\dfrac{1-\sqrt{3}}{3-\sqrt{3}}=\dfrac{-\sqrt{3}}{3}\)
Đúng 0
Bình luận (0)
c)\(TacoP>\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}>\dfrac{1}{2}\)
\(\Leftrightarrow2\sqrt{x}-2>\sqrt{x}+1\)
\(\Leftrightarrow\sqrt{x}>3\Leftrightarrow x>9\)
Vậy\(x>9\)Thì \(P>\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
















