Cho hình bình hành ABCD . Lấy M tuỳ ý trên cạnh BC . Gọi O là giao điểm của AM và BD
-Chứng minh rằng Sabcd = 2Smab
-Chứng minh rằng Sabo = Smod + Sbmc
Những câu hỏi liên quan
Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của BC và CD. Chứng minh rằng AM và AN chia đường chéo BD thành 3 phần bằng nhau
cho hình bình hành ABCD và O là giao điểm của AC và BD trên đường chéo AC lấy 2 điểm M và N sao cho AM=MN=NC
chứng minh tứ giác BMDN là hình bình hành
BC cắt DN tại K chứng minh N là trọng tâm của tam giác ABC
DC cắt BN tại I và AB cắt DM tại H chứng minh I,O,H thẳng hàng
1. Cho hình bình hành ABCD có AB 2AD. Gọi M, N theo tứ tự là trung điểm của các cạnh AB, CD. Gọi P và Q lần lượt là giao điểm của BN với CM và của AN với DMa. Tứ giác AMND là hình gì? Vì sao?b. Chứng minh: tứ giác MPNQ là hình chữ nhậtc. Tìm điều kiện của tứ giác ABCD để MPNQ là hình vuôngd. Chứng minh: bốn đường thẳng AC, BD, MN, QP đồng qui2. Cho hình bình hành ABCD. Kẻ AN, CM vuông góc với BD, N và M thuộc BDa. Chứng minh DN BM b. Ch...
Đọc tiếp
1. Cho hình bình hành ABCD có AB= 2AD. Gọi M, N theo tứ tự là trung điểm của các cạnh AB, CD. Gọi P và Q lần lượt là giao điểm của BN với CM và của AN với DM
a. Tứ giác AMND là hình gì? Vì sao?
b. Chứng minh: tứ giác MPNQ là hình chữ nhật
c. Tìm điều kiện của tứ giác ABCD để MPNQ là hình vuông
d. Chứng minh: bốn đường thẳng AC, BD, MN, QP đồng qui
2. Cho hình bình hành ABCD. Kẻ AN, CM vuông góc với BD, N và M thuộc BD
a. Chứng minh DN = BM
b. Chứng minh Tứ giác ANCM là hình bình hành
c. Gọi K là điểm đối xứng với A qua N. Tứ giác DKCB là hình gì? Vì sao?
d. Tia AM cắt tia KC tại P. Chứng minh các đường thẳng AC, PN, KM đồng qui
Cho tam giác ABC nội tiếp trong 1 đường tròn. M là điểm bất kì trên cung AC( không chứa điểm B). Kẻ MH vuông góc AC; Mk vuông góc BC. Gọi P,Q tương ứng là trung điểm của AB và KH. Chứng minh rằng tam giác PQM là tam giác vuôngCho hình vuông ABCD tâm O, cạnh hình vuông bằng 10cm. Gọi I là 1 điểm bất kì nằm trên nửa đường tròn đi qua 3 điểm A,O,D không chứa điểm O. IO cắt cạnh BC tại J. Cạnh DK của hình bình hành IJKD cắt BC tại E, EH là đường c...
Đọc tiếp
Cho tam giác ABC nội tiếp trong 1 đường tròn. M là điểm bất kì trên cung AC( không chứa điểm B). Kẻ MH vuông góc AC
; Mk vuông góc BC. Gọi P,Q tương ứng là trung điểm của AB và KH. Chứng minh rằng tam giác PQM là tam giác vuông
Cho hình vuông ABCD tâm O, cạnh hình vuông bằng 10cm. Gọi I là 1 điểm bất kì nằm trên nửa đường tròn đi qua 3 điểm A,O,D không chứa điểm O. IO cắt cạnh BC tại J. Cạnh DK của hình bình hành IJKD cắt BC tại E, EH là đường cao của tam giác EKJ.
a)Tính số đo của góc HEK
b) Chứng minh rằng IJ>10 căn 2 cm
BÀI 1: a) CHO HÌNH BÌNH HÀNH ABCD CÓ góc 90 . SO SÁNH AC VÀ BDb) TỨ GIÁC ABCD CÓ hat{A} , hat{B} ,hat{C} TÙ. CHỨNG MINH ACBDBÀI 2: CHO HÌNH CHỮ NHẬT ABCD. KẺ BH VUÔNG GÓC AC (H THUỘC AC). TRÊN TIA ĐỐI CỦA TIA BH LẤY ĐIỂM E SAO CHO BE AC. CHỨNG MINH RẰNG GÓC ADE 45 ĐỘBÀI 3 : CHỨNG MINH RẰNG TỨ GIÁC CÓ GIAO ĐIỂM HAI ĐƯỜNG CHÉO TRÙNG VỚI GIAO ĐIỂM CÁC ĐOẠN THẲNG NỐI TRUNG ĐIỂM CÁC CẠNH ĐỐI DIỆN THÌ TỨ GIÁC ĐÓ LÀ HÌNH BÌNH HÀNHBÀI 4: CHO TA...
Đọc tiếp
BÀI 1: a) CHO HÌNH BÌNH HÀNH ABCD CÓ góc >90 . SO SÁNH AC VÀ BD
b) TỨ GIÁC ABCD CÓ \hat{A} , \hat{B} ,\hat{C} TÙ. CHỨNG MINH AC<BD
BÀI 2: CHO HÌNH CHỮ NHẬT ABCD. KẺ BH VUÔNG GÓC AC (H THUỘC AC). TRÊN TIA ĐỐI CỦA TIA BH LẤY ĐIỂM E SAO CHO BE = AC. CHỨNG MINH RẰNG GÓC ADE = 45 ĐỘ
BÀI 3 : CHỨNG MINH RẰNG TỨ GIÁC CÓ GIAO ĐIỂM HAI ĐƯỜNG CHÉO TRÙNG VỚI GIAO ĐIỂM CÁC ĐOẠN THẲNG NỐI TRUNG ĐIỂM CÁC CẠNH ĐỐI DIỆN THÌ TỨ GIÁC ĐÓ LÀ HÌNH BÌNH HÀNH
BÀI 4: CHO TAM GIÁC ABC VUÔNG TẠI A ( AC > AB), ĐƯỜNG CAO AH. TRÊN TIA HC LẤY HD = HA, ĐƯỜNG VUÔNG GÓC VỚI BC TẠI D CẮT AC TẠI E.
a) CHỨNG MINH AE = AB
b) GỌI M LÀ TRUNG ĐIỂM BE . TÍNH GÓC AHM
BÀI 5: TỨ GIÁC ABCD CÓ CÓ GÓC A = GÓC B =90 ĐỘ VÀ AC = BD.
a) ABCD CÓ PHẢI LÀ HÌNH CHỮ NHẬT KHÔNG? C/M
b) LẤY ĐIỂM M NẰM GIỮA A,C. VẼ MK VUÔNG GÓC AB TẠI K , MH VUÔNG GÓC AD TẠI H. CHỨNG MINH HK // BD
C) TIA MH CẮT BC Ở E, TIA KM CẮT CD TẠI F. MD CẮT HF Ở I, MB CẮT KE TẠI J/ CHỨNG MINH HK + EF = 2IJ
đc có tí điểm bắt lm 5 câu dài ko ai muốn lm
Đúng 0
Bình luận (0)
cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD: a) chứng minh tứ giác AECF là hình bình hành b) DE cắt AC tại I, BF cắt AC tại K. Chứng minh rằng AI=IK=KC
Xem chi tiết
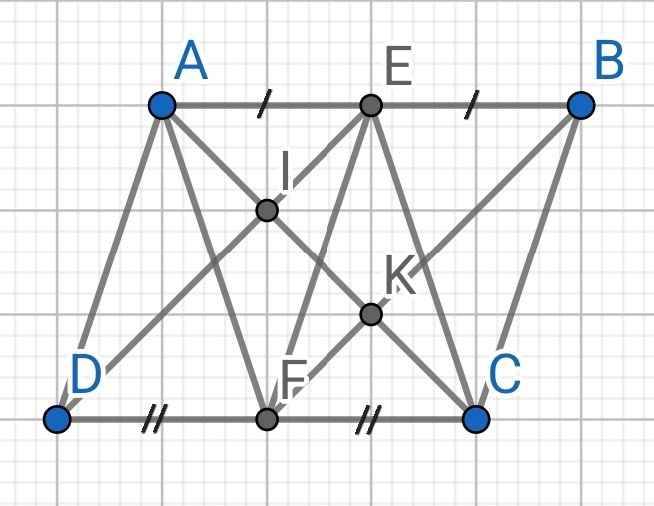a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC
Đúng 2
Bình luận (0)
cho hình bình hành ABCD. gọi E là trung điểm cùa AD, F là trung điểm của BC . chứng minh rằng BE=DF
ABCD là hình bình hành \(\Rightarrow\) AB = CD; góc A = góc C; AD = BC
E là trung điểm của AD \(\Rightarrow\) AE = \(\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow\) FC = \(\frac{BC}{2}\)
mà AD = BC (cmt)
nên AE = FC
Xét \(\Delta\) ABE và \(\Delta\) CDF có
góc A = góc C (cmt)
AE = FC (cmt)
AB = CD (cmt)
\(\Rightarrow\) tam giác ABE = tam giác CDF (c.g.c)
\(\Rightarrow\) BE = DF
Đúng 0
Bình luận (0)
cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD=1/2 DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI=IM
Gọi E là trung điểm DC
Xét tam giác BDC có:
E là trung điểm DC
M là trung điểm BC
=> EM là đường trung bình
=> EM//BD
=> EM//ID
Ta có: \(AD=\dfrac{1}{2}DC\)
Mà \(DE=\dfrac{1}{2}DC\)
\(\Rightarrow AD=DE=\dfrac{1}{2}AE\)=> D là trung điểm AE
Xét tam giác AME có:
D là trung điểm AE
ID//ME
=> I là trung điểm AM
=> AI=IM
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Một điểm I bất kì trên cạnh AB và một điểm M bất kì trên cạnh BC sao cho góc IEM =90 độ
a, chứng minh rằng tứ giác BIEM nội tiếp
b, Tính góc IME
c, Gọi N là giao điểm của tia AM với DC, K là giao điểm của BN và tia EM. Chứng minh CK vuông góc với BN