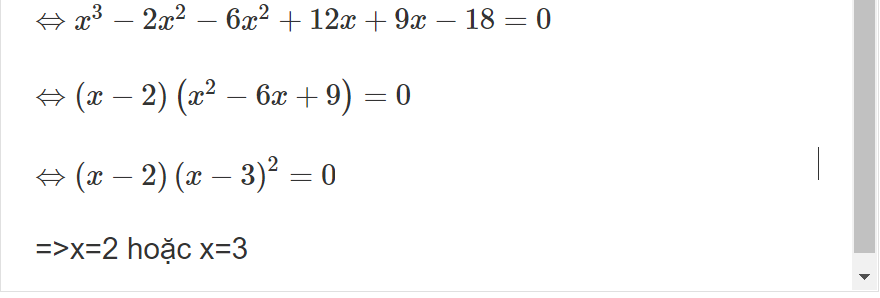\(\Leftrightarrow x^3-2x^2-6x^2+12x+9x-18=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-6x+9\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)

=>x=2 hoặc x=3

      x³ - 8.x² + 21.x - 18 = 0  

<=> x³ - 2.x² -6.x² +12.x +  9.x -18 = 0

<=> x² . (x-2 )  - 6.x . ( x - 2 ) + 9.(x - 2 ) =0

<=> (x-2 ) . ( x² - 6.x + 9 )       = 0

<=> (x-2 ) . ( x-3 )²       = 0

<=> \(\orbr{\begin{cases}x-2=0\\\left(x-3\right)^2=0\end{cases}}\)   

<=> \(\orbr{\begin{cases}x=2\\x=3\end{cases}}\)

Vậy phương trình trên có tập nghiệm { 2;3 }

\(x^3-8x^2+21x-18=0\)

\(\Leftrightarrow x^3-2x^2-6x^2+12x+9x-18=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-6x+9\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)

\(x^3-8x^2+21x-18=0\)

\(\left(x^2-6x+9\right)\left(x-2\right)=0\)

\(\left(x-3\right)^2\left(x-2\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=2\end{cases}}}\)

g: =>(x-1)(x-2)=0

=>x=1 hoặc x=2

i: \(\Leftrightarrow x^4-x^3+x^3-x^2+2x^2-2x+8x-8=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+2x+8\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-x+4\right)=0\)

=>x=1 hoặc x=-2

g) x^2 - 3x + 2 = 0

<=> x^2 - 2x-x+2 =0

<=> x=1 hoặc x = 2

..tự kết luận

i)x^4 + x^2 + 6x - 8=0

<=> x^4 + 2x^3 - 2x^3 - 4x^2 + 5x^2 + 10x - 4x - 8 = 0

<=> x^3(x + 2) - 2x^2(x+2) + 5x(x+2) - 4(x+2) = 0

<=> (x^3 - 2x^2 +5x -4)(x+2)=0

<=> (x^3 - x^2 -x^2 +x + 4x - 4)(x+2) = 0

<=>(x^2(x-1) - x(x-1) + 4(x-1) )(x+2) = 0

<=> (x^2-x+4)(x-1)(x+2)=0

<=> x = 1 hoặc x +-2 hoặc x^2 - x+4=0

                                     <=>x^2 - x+ 1/4 - 1/4 +4=0

                                      <=>(x-1/2)^2 +15/4=0

                                     <=>(x-1/2)^2=-15/4 (vô lí)

....tự kết luận

h)x^3 - 8x^2 + 21x - 18 = 0

<=> x^3 - 2x^2 - 6x^2 + 12x + 9x - 18 = 0

<=> x^2(x-2) -6x(x-2) + 9(x-2) =0

<=>(x-3)^2(x-2)=0

<=> x=3 hoặc x =2 

...tự kết luận

g: \(x^2-3x+2=0\)

=>(x-1)(x-2)=0

=>x=1 hoặc x=2

i: \(x^4+x^2+6x-8=0\)

\(\Leftrightarrow x^4-x^3+x^3-x^2+2x^2-2x+8x-8=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+2x+8\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left[\left(x+2\right)\left(x^2-2x+4\right)+x\left(x+2\right)\right]=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-x+4\right)=0\)

=>x=1 hoặc x=-2

h) \(x^3-8x^2+21x-18=0\)

\(\Leftrightarrow x^3-2x^2+6x^2-12x+9x-18=0\)

\(\Leftrightarrow x^2\left(x-2\right)+6x\left(x-2\right)+9\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+6x+9\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+3\right)^2=0\)

\(\Leftrightarrow x-2=0\) hay \(x+3=0\)

\(\Leftrightarrow x=2\) hay \(x=-3\)

(x^3-9x^2+27x-27)+(x^2-6x+9)=0

(x-3)^3+(x-3)^2=0

(x-3)^2(x-2)=0

<=>x-3=0 hoặc x-2=0

<=>x=3 hoặc x=2

câu a) x=-3 nữa nha

a) x³ - 8x² + 21x - 18 = 0

<=> (x - 2)(x - 3)(x - 3) = 0

<=> x - 2 = 0 hoặc x - 3 = 0

<=> x = 2 hoặc x = 3

Vậy: phương trình có tập nghiệm là: S = {2, 3}

b) x⁴ + x² + 6x - 8 = 0

<=> (x - 1)(x + 2)(x² - x + 4) = 0

vì x² - x + 4 # 0 nên:

<=> x - 1 = 0 hoặc x + 2 = 0

<=> x = 1 hoặc x = -2

Vậy: phương trình có tập nghiệm là: S = {1, -2}