Cho (O), I là trung điểm dây AB. Kẻ CD là 1 dây bất kì đi qua I, ko trùng với BA. CM: AB<CD.

Những câu hỏi liên quan
Cho (O) và dây AB . Gọi M là trung điểm của dây AB . Vẽ dây CD bất kì đi qua M (CD là dây ko trùng với AB) Kẻ OH vuông góc CD tại H
SO sánh OM và OH
Chứng minh dây CD dài hơn dây AB
GIÚP MÌNH NHA CẢM ƠN NHÌU
Cho đường tròn tâm O đường kính AB. Dây CD bất kì vuông góc với AB tại H. I là trung điểm DH. K là đối xứng của H qua D. Dây MN bất kì đi qua I. CM 4 điểm K, H, M, N cùng thuộc 1 đường tròn
CHo đường tròn (O ; R ) và dây AB = 8 cm . Gọi I là điểm thuộc dây AB sao cho AI = 1 cm . Kẻ dây CD đi qua I và vuông góc với AB .
Chứng minh : CD = AB
Cho (O ; 5cm),dây AB = 8cm.
a.Tính khoảng cách từ O đến dây AB.
b.Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB.Chứng minh CD = AB
Giải thích các bước giải:
a.Gọi MM là trung điểm
Đúng 1
Bình luận (0)
a: Gọi OM là khoảng cách từ O đến AB
Suy ra: M là trung điểm của AB
hay \(AM=BM=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOMA vuông tại M, ta được:
\(OA^2=OM^2+MA^2\)
\(\Leftrightarrow OM^2=5^2-4^2=9\)
hay OM=3(cm)
Đúng 1
Bình luận (0)
(ko cần vẽ hình)Cho đường tròn (O) có bán kính 5cm, dây AB 8cm. Gọi I là điểm thuộc dây AB sao cho AI 1cm. Kẻ dây CD đi qua I và vuông góc với AB (C thuộc cung nhỏ AB)a) Tính khoảng cách từ tâm O đến dây ABb) Chứng minh rằng: CD ABc) Chứng minh rằng:i. IO là tia phân giác của góc tạo bởi hai đường thẳng AB và CD ii. IO vuông góc với AC và BDd) Chứng minh rằng: IA IC; IB ID; BC AD. Tính T IA^2+IB^2+IC^2+ID^2
Đọc tiếp
(ko cần vẽ hình)Cho đường tròn (O) có bán kính 5cm, dây AB = 8cm. Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB (C thuộc cung nhỏ AB)a) Tính khoảng cách từ tâm O đến dây ABb) Chứng minh rằng: CD = ABc) Chứng minh rằng:i. IO là tia phân giác của góc tạo bởi hai đường thẳng AB và CD
ii. IO vuông góc với AC và BD
d) Chứng minh rằng: IA = IC; IB = ID; BC = AD. Tính T = \(IA^2+IB^2+IC^2+ID^2\)
Bài 4(3 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C bất kỳ trên đường tròn (O; R) (C không trùng A; AC BC). Qua C kẻ dây CD của đường tròn (O; R) vuông góc với đường kính AB tại I. Lấy điểm E sao cho I là trung điểm AE. Tia DE cắt đoạn thẳng BC tại F. Gọi K là trung điểm của BE. 1) Chứng minh tam giác BCD cân. 2) Chứng minh AC I/ DE và chứng minh F thuộc đường tròn tâm K đường kính BE. 3) Chứng minh IF là tiếp tuyến của đường tròn tâm K đường kính BE. 4) Lấy điểm M trên đoạn thẳng O...
Đọc tiếp
Bài 4(3 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C bất kỳ trên đường tròn (O; R) (C không trùng A; AC < BC). Qua C kẻ dây CD của đường tròn (O; R) vuông góc với đường kính AB tại I. Lấy điểm E sao cho I là trung điểm AE. Tia DE cắt đoạn thẳng BC tại F. Gọi K là trung điểm của BE. 1) Chứng minh tam giác BCD cân. 2) Chứng minh AC I/ DE và chứng minh F thuộc đường tròn tâm K đường kính BE. 3) Chứng minh IF là tiếp tuyến của đường tròn tâm K đường kính BE. 4) Lấy điểm M trên đoạn thẳng OC sao cho OM = CI. Chứng minh khi điểm C di chuyển trên nửa đường tròn (O; R) không chứa điểm D (C khác A, B) thì điểm M chạy trên một đường tròn cố định.
Cho một điểm I nằm bên trong đường tròn (O). Qua I kẻ một dây AB bất kì và kẻ dây CD vuông góc với OI, OI kéo dài cắt đường tròn (O) ở E. Bán kính OF vuông góc với AB tại H.
a) So sánh AB và CD.
b) So sánh IE và HF.
a CD <AB,b IE=OE-OI=OF-OI<OF-OH=HF
a) CD<AB,b)IE=OE-OI=OF-OI<OF-OH=HF
a/ Xét vuông tại :
(cạnh góc vuông<cạnh huyền)
Xét :
là đường vuông góc dây
là đường vuông góc dây
mà
b/ Vì
là bán kính
mà là bán kính
Ta có:
hay
Vậy
Xem thêm câu trả lời
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.
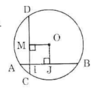
Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: 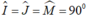 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và I là trung điểm của một dây AB. Hai dây bất kì CD và EF đi qua I với EF > CD; CF và ED cắt AB tại M và N. Vẽ dây FG // AB.
a. Chứng minh tam giác IFG cân .
b. Chứng minh rằng tứ giác INDG nội tiếp được trong đường tròn.
c. Chứng minh rằng IM = IN


















