Cho tam giác ABC có các góc đều nhọn. Ba đường cao AD, BE, CF đồng qui tại H. Chứng minh rằng: AH.DH=BH.EH=CH.FH

Những câu hỏi liên quan
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.
Chứng rằng : \(AH.DH=BH.EH=CH.FH\)
Cho tam giác ABC có ba đường cao AD,BE,CF đồng quy tại H .CMR: AH.DH=BH.EH=CH.FH
Cho tam giác ABC . Ba đường cao AD , BE , CF cắt tại H . Chứng minh AH.DH=BH.EH=CH.FH
Xét ΔAFH vuông tại F và ΔCDH vuông tại D có
\(\widehat{AHF}=\widehat{CHD}\)
Do đó: ΔAFH\(\sim\)ΔCDH
Suy ra: HA/HC=HF/HD
hay \(HA\cdot HD=HF\cdot HC\left(1\right)\)
Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)
Do đó: ΔFHB\(\sim\)ΔEHC
Suy ra: HB/HC=HF/HE
hay \(HB\cdot HE=HF\cdot HC\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HD=HB\cdot HE=HC\cdot HF\)
Đúng 0
Bình luận (0)
Bài 8 (1,0 đ): Cho tam giác ABC nhọn kẻ ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh: AH.DH+BH.EH=2CH.FH
Xét ΔHFA vuông tại F và ΔHDC vuông tại D có
góc FHA=góc DHC
=>ΔHFA đồng dạng với ΔHDC
=>HF/HD=HA/HC
=>HF*HC=HD*HA
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE
=>AH*DH+BH*EH=2*CH*FH
Đúng 0
Bình luận (0)
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.Chứng minh rằng:AH.DH = BH.EH = CH.FH
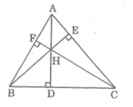
Xét △ AFH và △ CDH, ta có:
∠ (AFH) = ∠ (CDH) = 90 0
∠ (AHF) = ∠ (CHD) (đối đỉnh)
Suy ra: △ AFH đồng dạng △ CDH (g.g)
Suy ra: 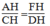
Suy ra: AH.DH = CH.FH (1)
Xét △ AEH và △ BDH,ta có:
∠ (AEH) = ∠ (BDH) = 90 0
∠ (AHE) = ∠ (BHD) (đối đỉnh)
Suy ra: △ AEH đồng dạng △ BDH (g.g)
Suy ra: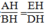
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Có tam giác ABE đồng dạng tam giác ACF, tam giác AEF đồng dạng tam giác ABC. Chứng minh:
a) tam giác HEF đồng dạng tam giác HBC.
b) H là giao 3 đường phân giác của tam giác HEF.
c) AH.DH = BH.EH = CH.FH.
d) BH.BE + CH.CF = \(BC^2\)
Toán 8 ôn tập trường hợp đồng dạng của tam giác nha
ko phải lớp 9 nha.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Có tam giác ABE đồng dạng tam giác ACF, tam giác AEF đồng dạng tam giác ABC. Chứng minh:
a) tam giác HEF đồng dạng tam giác HBC.
b) H là giao 3 đường phân giác của tam giác HEF.
c) AH.DH = BH.EH = CH.FH.
d) BH.BE + CH.CF = \(BC^2\)
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H. 1) Chứng minh rằng: AE.AC AF.AB2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC4) Chứng minh rằngBF.BA+CE.CA BC2
Đọc tiếp
) Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
1) Chứng minh rằng: AE.AC = AF.AB
2) Chứng minh rằng tam giác AFE đồng dạng tam giác ACB
3) Chứng minh rằng tam giác FHE đồng dạng tam giác BHC
4) Chứng minh rằngBF.BA+CE.CA = BC2
1: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
2: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng vơi ΔABC
3: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF/HB=HE/HC
Xét ΔHFE và ΔHBC có
HF/HB=HE/HC
góc FHE=góc BHC
=>ΔFHE đồng dạng với ΔBHC
Đúng 1
Bình luận (0)
Cho tam giác ABC, các đường cao AD, BE và CF. Gọi H là trực tâm của tam giác.chứng minh:AH.DH=BH.EH=CH.FH















