Giải và biện luận hệ phương trình
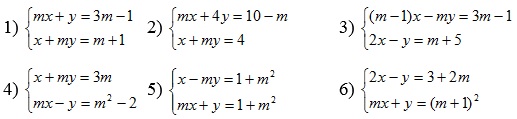
Giải và biện luận theo tham số m hệ phương trình:
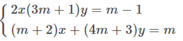
Nhân phương trình thứ nhất của hệ với m + 2, nhân phương trình thứ hai với 2 ta được hệ phương trình
![]()
Trừ hai phương trình vế theo vế ta được phương trình:
(3m2 - m - 4)y = (m + 1)(m + 2) (1)
+ Với m = -1 phương trình (1) có dạng: 0y = 0
Phương trình này nhận mọi giá trị thức của y làm nghiệm. Lúc đó thay m = -1 vào hệ phương trình đã cho, hai phương trình trở thành một phương trình.
x - y = 1 ⇒ y = x + 1, x tùy ý.
+ Với m = 4/3 phương trình (1) có dạng: 0y = -14/9
Phương trình này vô nghiệm, do đó hệ phương trình đã cho vô nghiệm.
+ Với m ≠ -1 và m ≠ 4/3, phương trình (1) có nghiệm duy nhất
![]()
Thay vào một trong hai phương trình của hệ đã cho ta suy ra
![]()
Kết luận
m = 4/3: Hệ phương trình đã cho vô nghiệm.
m = -1: Hệ phương trình đã cho có vô số nghiệm
x = a, y = a + 1, a là số thực tùy ý.
m ≠ 1, m ≠ 4/3: Hệ phương trình đã cho có nghiệm duy nhất :
![]()
Giải giúp em với ạ:
Cho hệ phương trình: mx + 4y = 10 - m và x + my = 4 (m là tham số)
a, giải hệ phương trình khi m = √2
b, giải và biện luận hệ phương trình theo m
Cô làm câu b thôi nhé :)
Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)
Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)
Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.
Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)
Từ đó : \(x=\frac{8-m}{2+m}\)
Kết luận:
+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
+ m = - 2, hệ phương trình vô nghiệm.
+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)
Chúc em học tập tốt :)

hehe
Hỏi từ lâu nhưng bây giờ em trả lời lại cho vui
Cho hệ phương trình: { 2mx + y = 2 (m mà than số)
{ 8x + my = m + 2
a) Giải hệ phương trình khi m = -1
b) Tìm m để hệ phương trình có nghiệm là x = 2; y = 6
c) Giải và biện luận hệ phương trình theo m
d) Trong trường hợp có nghiệm duy nhất:
+ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc m
+ Tìm m để 4x + 3y = 7
+ Tìm m để x - y > 0
+ Tìm m để P = y^2 - 2x đạt giá trị nhỏ nhất
Cho hệ phương trình \(|^{mx+2y=1}_{3x+\left(m+1\right)y=-1}\) (với m là tham số)
a) Giải hệ phương trình với m = 3.
b) Giải và biện luận hệ phương trình theo m.
c) Tìm m để hệ phương trình có nghiệm là số nguyên.
Cho hệ phương trình \(\left\{{}\begin{matrix}x-2y=1\\mx+y=2\end{matrix}\right.\)
giải và biện luận hệ phương trình với m là tham số
• PT có nghiệm duy nhất \( \Leftrightarrow \dfrac{1}{m} \ne \dfrac{-2}{1} \Leftrightarrow m \ne \dfrac{-1}{2}\)
• PT vô nghiệm \(\Leftrightarrow \dfrac{1}{m} =\dfrac{-2}{1} \ne \dfrac{1}{2} \Leftrightarrow m=\dfrac{-1}{2}\)
• PT có vô số nghiệm \(\Leftrightarrow \dfrac{1}{m} = \dfrac{-2}{1} = \dfrac{1}{2} (\text{Vô lý})\)
Vậy....
nêu chi tiết phương pháp giải và biện luận hệ phương trình lớp 9
tính m theo 3 trường hợp của denta hoặc denta phẩy
1, Giải và biện luận theo số nguyên m phương trình vô định sau đây
3x+(2m-1)y=m+1.
2,Giải và biện luận theo số nguyên m hệ
phương trình vô định sau đây
\(\left\{{}\begin{matrix}3x+2y=1\\3x+6y+\left(m+1\right)z=m-2\end{matrix}\right.\)
Cho hệ phương trình (m là tham số): 2mx+y=2 8x+my=m+2 Giải và biện luận hệ phương trình đã cho theo m Mn giúp em với ạ
2mx+y=2 và 8x+my=m+2
=>y=2-2mx và 8x+m(2-2mx)=m+2
=>\(\left\{{}\begin{matrix}8x+2m-2m^2x-m-2=0\\y=-2mx+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(-2m^2+8\right)=-m+2\\y=-2mx+2\end{matrix}\right.\)
=>2(m-2)(m+2)x=m-2 và y=-2mx+2
Nếu m=2 thì hệpt có vô số nghiệm
Nếu m=-2 thìhệ pt vn
Nếu m<>2; m<>-2 thì hệ phương trình có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{1}{2\left(m+2\right)}\\y=-2m\cdot\dfrac{1}{2\left(m+2\right)}+2=-\dfrac{m}{m+2}+2=\dfrac{-m+2m+4}{m+2}=\dfrac{m+4}{m+2}\end{matrix}\right.\)
Cho hệ phương trình:
\(\hept{\begin{cases}2x-my=m^2\\x+y=2\end{cases}}\)
a)giải hệ khi m=1
b) giải và biện luận hệ phương trình