1a) Để \(\frac{6x+5}{2x+1}\)là số nguyên thì 6x+5 chia hết cho 2x+1

=> (6x+3)+2 chia hết cho 2x+1

=> 2 chia hết cho 2x+1 ( vì 6x+3 chia hết cho 2x+1)

=> 2x+1 thuộc ước của 2={ 1;-1;2;-2}

Với 2x+1=1=> x=0

Với 2x+1=-1=> x=-1

Với 2x+1=...........

Với 2x+1=.......

Vậy x=.............

b) Để \(\frac{3x+9}{x-4}\)là số nguyên thì 3x+9 chia hết cho x-4

=> (3x-12)+21 chia hết x-4

=> 21 chia hết cho x-4 ( vì 3x-12 chia hết cho x-4)

=> x-4 thuộc Ư(12)={1;-1;2;-2;3;-3;4;-4;6;-6;12;-12}

Với x-4=1=> x=5

Với x-4=-1=> x=3

....

....

....

....

...

Vậy x=......

2) \(\left(x+\frac{1}{2}+x+\frac{1}{3}\right)+\left(2x+\frac{1}{3}+2x+\frac{1}{4}\right)=0\)

=> \(6x+\frac{17}{12}=0\)

=> \(x=\frac{0-\frac{17}{12}}{6}=-\frac{89}{12}\)

Đúng rồi

a) Ta có: \(A=\dfrac{2x}{x+3}+\dfrac{x+1}{x-3}+\dfrac{3-11x}{9-x^2}\)

\(=\dfrac{2x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{11x-3}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{2x^2-6x+x^2+4x+3+11x-3}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{3x^2+9x}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{3x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x}{x-3}\)

b)

ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)

Ta có: P=AB

\(=\dfrac{3x}{x-3}\cdot\dfrac{x-3}{x+1}\)

\(=\dfrac{3x}{x+1}\)

Để \(P=\dfrac{9}{2}\) thì \(\dfrac{3x}{x+1}=\dfrac{9}{2}\)

\(\Leftrightarrow9\left(x+1\right)=6x\)

\(\Leftrightarrow9x-6x=-9\)

\(\Leftrightarrow3x=-9\)

hay x=-3(loại)

Vậy: Không có giá trị nào của x để \(P=\dfrac{9}{2}\)

A = \(6\)

bạn có thể giải chi tiết giúp mình đc ko

MK ko biế đúng ko nữa , sai thì ý kiến

a)

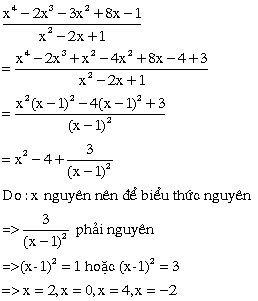
b)

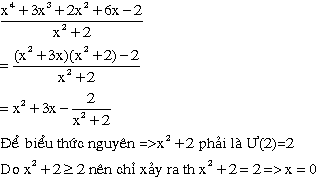
Chúc các bn hok tốt

Tham khảo nhé

(a) \(f\left(x\right)⋮g\left(x\right)\Rightarrow\dfrac{x^2-5x+9}{x-3}\in Z\)

Ta có: \(\dfrac{x^2-5x+9}{x-3}\left(x\ne3\right)=\dfrac{x\left(x-3\right)-2\left(x-3\right)+3}{x-3}=x-2+\dfrac{3}{x-3}\)nguyên khi và chỉ khi: \(\left(x-3\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

\(\Rightarrow\left[{}\begin{matrix}x-3=1\\x-3=-1\\x-3=3\\x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\\x=6\\x=0\end{matrix}\right.\) (thỏa mãn).

Vậy: \(x\in\left\{0;2;4;6\right\}\).

(b) \(f\left(x\right)⋮g\left(x\right)\Rightarrow\dfrac{2x^3-x^2+6x+2}{2x-1}\in Z\left(x\ne\dfrac{1}{2}\right)\)

Ta có: \(\dfrac{2x^3-x^2+6x+2}{2x-1}=\dfrac{x^2\left(2x-1\right)+3\left(2x-1\right)+5}{2x-1}=x^2+3+\dfrac{5}{2x-1}\)

nguyên khi và chỉ khi: \(\left(2x-1\right)\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)

\(\Rightarrow\left[{}\begin{matrix}2x-1=1\\2x-1=-1\\2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\\x=3\\x=-2\end{matrix}\right.\) (thỏa mãn).

Vậy: \(x\in\left\{-2;0;1;3\right\}\).

a: f(x) chia hết cho g(x)

=>x^2-3x-2x+6+3 chia hết cho x-3

=>3 chia hết cho x-3

=>x-3 thuộc {1;-1;3;-3}

=>x thuộc {4;2;6;0}

b: f(x) chia hết cho g(x)

=>2x^3-x^2+6x-3+5 chia hết cho 2x-1

=>5 chia hết cho 2x-1

=>2x-1 thuộc {1;-1;5;-5}

=>x thuộc {2;0;3;-2}

ĐKXĐ: \(x\ne1\)

Ta có: \(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)

\(=\dfrac{x^4-2x^3+x^2-4x^2+8x-4+3}{x^2-2x+1}\)

\(=\dfrac{x^2\left(x^2-2x+1\right)-4\left(x^2-2x+1\right)+3}{x^2-2x+1}\)

\(=\dfrac{\left(x-1\right)^2\cdot\left(x^2-4\right)+3}{\left(x-1\right)^2}\)

\(=x^2-4+\dfrac{3}{\left(x-1\right)^2}\)

Để B nguyên thì \(3⋮\left(x-1\right)^2\)

\(\Leftrightarrow\left(x-1\right)^2\inƯ\left(3\right)\)

\(\Leftrightarrow\left(x-1\right)^2\in\left\{1;3;-1;-3\right\}\)

mà \(\left(x-1\right)^2>0\forall x\) thỏa mãn ĐKXĐ

nên \(\left(x-1\right)^2\in\left\{1;3\right\}\)

\(\Leftrightarrow x-1\in\left\{1;9\right\}\)

hay \(x\in\left\{2;10\right\}\) (nhận)

Vậy: \(x\in\left\{2;10\right\}\)