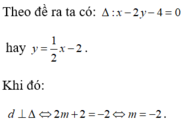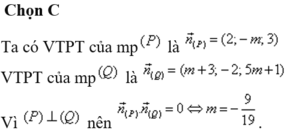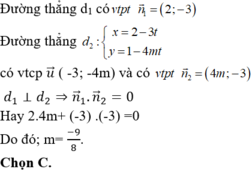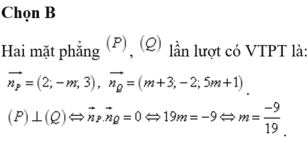Với giá trị nào của m thì 2 đường thẳng sau vuông góc(1-2m)x-my+10=0,-3x-2y+6=0

Những câu hỏi liên quan
Với giá trị nào của m thì đường thẳng Δ:3x– y+ 2m=0 tiếp xúc với đường tròn (C): x²+ y²+ 6x– 2y=0
(C); x^2+6x+y^2-2y=0
=>x^2+6x+9+y^2-2y+1=10
=>(x+3)^2+(y-1)^2=10
=>I(-3;1); \(R=\sqrt{10}\)
Để Δ tiếp xúc vơi (C) thì d(I;Δ)=căn 10
=>\(\dfrac{\left|-3\cdot3+1\cdot\left(-1\right)+2m\right|}{\sqrt{3^2+\left(-1\right)^2}}=\sqrt{10}\)
=>|2m-10|=10
=>2m-10=10 hoặc 2m-10=-10
=>m=0 hoặc m=10
Đúng 1
Bình luận (0)
Cho hàm số
y
-
x
3
+
3
x
2
+
(
2
m
-
1
)
x
+
2
m
-
3
có đồ thị (Cm). Với giá trị nào của tham số m thì tiếp tuyến của hệ số góc lớn nhất của đồ thị (Cm) vuông góc với đường thẳng
△
:
x
-
2
y
-
4...
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 + ( 2 m - 1 ) x + 2 m - 3 có đồ thị (Cm). Với giá trị nào của tham số m thì tiếp tuyến của hệ số góc lớn nhất của đồ thị (Cm) vuông góc với đường thẳng △ : x - 2 y - 4 = 0 ?
A. m=-2
B. m=-1
C. m=0
D. m=4
Với giá trị nào của m thì hai đường thẳng d1: 3x+ 4y+ 10 0 và d2: (2m-1) x+ m2y + 10 0 trùng nhau ? A. m ∈ ∅ B.m -2 C.m 2 D.mọi m
Đọc tiếp
Với giá trị nào của m thì hai đường thẳng d1: 3x+ 4y+ 10= 0 và d2: (2m-1) x+ m2y + 10= 0 trùng nhau ?
A. m ∈ ∅
B.m= -2
C.m= 2
D.mọi m
Để 2 đường thẳng đã cho trùng nhau khi và chỉ khi
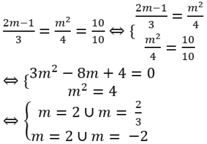
Tương đương m= 2.
Chọn C.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, với giá trị nào của m thì đường thẳng △: (2m-1)x+my-10=0 vuông góc với đường thẳng △': 3x+2y+6=0
?
\(\overrightarrow{n_d}=\left(2m-1;m\right)\) ; \(\overrightarrow{n_{d'}}=\left(3;2\right)\)
\(d\perp d'\Rightarrow\overrightarrow{n_d}.\overrightarrow{n_{d'}}=0\Rightarrow3\left(2m-1\right)+2m=0\Rightarrow m=\frac{3}{8}\)
Đúng 0
Bình luận (0)
Tìm giá trị của m để cặp mặt phẳng sau vuông góc (P) 2x-my+3z-6+m0 và (Q) (m+3)x-2y+(5m+1)-100. Tìm giá trị thực m để mặt phẳng (P) vuông góc với (Q) A. m1 B.
m
≠
1
C.
m
-
9
19
D.
m
-
5
2
Đọc tiếp
Tìm giá trị của m để cặp mặt phẳng sau vuông góc (P) 2x-my+3z-6+m=0 và (Q) (m+3)x-2y+(5m+1)-10=0. Tìm giá trị thực m để mặt phẳng (P) vuông góc với (Q)
A. m=1
B. m ≠ 1
C. m = - 9 19
D. m = - 5 2
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10 0 và
d
2
:
x
2
-
3
t
y
1
-
4
m
t...
Đọc tiếp
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
![]()
![]()
![]()
![]()
Với giá trị nào của m hai đường thẳng sau đây vuông góc nhau ? ∆1 : mx+ y-19 0 và ∆2 : (m-1) x+ (m+1) y-20 0 A. Mọi m. B.m 1 C. Không có m. D. m -1
Đọc tiếp
Với giá trị nào của m hai đường thẳng sau đây vuông góc nhau ?
∆1 : mx+ y-19 = 0 và ∆2 : (m-1) x+ (m+1) y-20 = 0
A. Mọi m.
B.m= 1
C. Không có m.
D. m= -1
Đường thẳng Δ1 có vectơ pháp tuyến là ![]() .
.
Đường thẳng Δ2 có vectơ pháp tuyến là ![]() .
.
Hai đường thẳng vuông góc khi và chỉ khi ![]()
Suy ra : m( m-1) + m+ 1= 0 hay m2+1 = 0 phương trình vô nghiệm.
Vậy không có giá trị của m để hai đường thẳng vuông góc.
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian Oxyz , cho hai mặt phẳng (P) 2x-my+3z+6+m0, (Q) (m+3)x-2y+(5m+1)-100. Tìm giá trị thực của m để mặt phẳng (P) vuông góc với (Q) A. m1 B.
m
-
9
19
C.
m
≠
1
D.
m
-
5
2
Đọc tiếp
Trong không gian Oxyz , cho hai mặt phẳng (P) 2x-my+3z+6+m=0, (Q) (m+3)x-2y+(5m+1)-10=0. Tìm giá trị thực của m để mặt phẳng (P) vuông góc với (Q)
A. m=1
B. m = - 9 19
C. m ≠ 1
D. m = - 5 2
Cho phương trình
x
2
+
y
2
+
m
−
3
x
+
2
m
+
1
y
+
3
m
+
10
0
.Giá trị của m để phương trình trên là ph...
Đọc tiếp
Cho phương trình x 2 + y 2 + m − 3 x + 2 m + 1 y + 3 m + 10 = 0 .Giá trị của m để phương trình trên là phương trình của một đường tròn có tâm nằm trên đường thẳng ∆: x + 2y + 5 = 0 là:
A.m = 0
B.m = 11/5
C.m = 2
D.không tồn tại m
Điều kiện để phương trình đã cho là phương trình đường tròn là:
m − 3 2 2 + 2 m + 1 2 2 − ( 3 m + 10 ) > 0 ⇔ m 2 − 6 m + 9 4 + 4 m 2 + 4 m + 1 4 − 3 m − 10 > 0 ⇔ 5 m 2 − 2 m + 10 4 − 3 m − 10 > 0 ⇔ 5 m 2 − 2 m + 10 − 12 m − 40 > 0 ⇔ 5 m 2 − 14 m − 30 > 0 ⇔ m < 7 − 199 5 m > 7 + 199 5
Với điều kiện trên phương trình đã cho là phương trình đường tròn có tâm I − m − 3 2 ; − 2 m + 1 2
Do tâm I nằm trên đường thẳng ∆: x + 2y + 5 = 0 nên ta có:
− m − 3 2 + 2. − 2 m + 1 2 + 5 = 0 ⇔ − ( m − 3 ) + 2 ( − 2 m − 1 ) + 2.5 = 0 ⇔ − m + 3 − 4 m − 2 + 10 = 0 ⇔ − 5 m + 11 = 0 ⇔ m = 11 5
Kết hợp điều kiện, suy ra không có giá trị nào của m thỏa mãn,
Chú ý. Nhiều học sinh quên điều kiện để phương trình là phương trình của một đường tròn nên dẫn đến kết quả m = 11/5
ĐÁP ÁN D
Đúng 0
Bình luận (0)