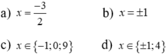giải phương trình :x3-9x2-11=0

Những câu hỏi liên quan
Giải các phương trình sau:a)
x
+
2
3
+
x
+
1
3
0
;
b)
2
x
4
+
3
x
2
−
5
0
;
c)
x...
Đọc tiếp
Giải các phương trình sau:
a) x + 2 3 + x + 1 3 = 0 ;
b) 2 x 4 + 3 x 2 − 5 = 0 ;
c) x 4 − 8 x 3 − 9 x 2 = 0 ;
d) x 3 − 4 x 2 + 4 − x = 0 .
Giải bất phương trình: 9 x 2 + 4 x – 3 – 3 x + 2 2 > 0
9x2 + 4x – 3 – (3x + 2)2 > 0
⇔9x2 + 4x – 3 – (9x2 + 12x + 4) > 0
⇔ 9x2 + 4x – 3 – 9x2 – 12x – 4 > 0
⇔ – 8x > 7 ⇔ x < 7/-8 ⇔ x < -7/8
Tập nghiệm: S = {x|x < -7/8}
Đúng 0
Bình luận (0)
Giải phương trình
e) x4 -4x3-8x2+8x=0
f) 2x2+3xy+y2=0
g) 2x4-x3-9x2+13x-5=0
h) (x+1)(x+3)(x+5)(x+7)+15=0
e: =>x(x^3-4x^2-8x+8)=0
=>x[(x^3+8)-4x(x+2)]=0
=>x(x+2)(x^2-2x+4-4x)=0
=>x(x+2)(x^2-6x+4)=0
=>\(x\in\left\{0;-2;3+\sqrt{5};3-\sqrt{5}\right\}\)
g: =>2x^4+5x^3-6x^3-15x^2+6x^2+15x-2x-5=0
=>(2x+5)(x^3-3x^2+3x-1)=0
=>(2x+5)(x-1)^3=0
=>x=1 hoặc x=-5/2
h: =>(x^2+8x+7)(x^2+8x+15)+15=0
=>(x^2+8x)^2+22(x^2+8x)+120=0
=>(x^2+8x+10)(x^2+8x+12)=0
=>(x^2+8x+10)(x+2)(x+6)=0
=>\(x\in\left\{-2;-6;-4+\sqrt{6};-4-\sqrt{6}\right\}\)
Đúng 0
Bình luận (0)
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
9x2 – 12x + 4 = 0
Phương trình 9x2 – 12x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ’ = (-6)2 – 4.9 = 0
⇒ Phương trình có nghiệm kép x1 = x2.
Theo hệ thức Vi-et ta có: 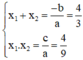
Đúng 0
Bình luận (0)
giải phương trình sau:
a. (9x2-4)(x+1) = (3x+2) (x2-1)
b. (x-1)2-1+x2 = (1-x)(x+3)
c. (x2-1)(x+2)(x-3) = (x-1)(x2-4)(x+5)
d. x4+x3+x+1=0
e. x3-7x+6 = 0
f. x4-4x3+12x-9 = 0
g. x5-5x3+4x = 0
h. x4-4x3+3x2+4x-4 = 0
m.n jup vs
Tìm x :
a ) 2(x2+8x+16) -x2+4 = 0
b ) x3-9x2+19x-11=0
x3 - 9x2 + 19x - 11 = 0
<=> (x - 1)(x2 - 8x + 11) = 0
<=> x - 1 = 0
<=> x = 1
Giải các phương trình sau:a, (9x2 - 4)(x + 1) (3x +2)(x2 - 1)b, (x - 1)2 - 1 + x2 (1 - x)(x + 3)c, (x2 - 1)(x + 2)(x - 3) (x - 1)(x2 - 4)(x + 5)d, x4 + x3 + x + 1 0e, x3 - 7x + 6 0f, x4 - 4x3 + 12x - 9 0g, x5- 5x3 + 4x 0h, x4 - 4x3 + 3x2 + 4x - 4 0
Đọc tiếp
Giải các phương trình sau:
a, (9x2 - 4)(x + 1) = (3x +2)(x2 - 1)
b, (x - 1)2 - 1 + x2 = (1 - x)(x + 3)
c, (x2 - 1)(x + 2)(x - 3) = (x - 1)(x2 - 4)(x + 5)
d, x4 + x3 + x + 1 = 0
e, x3 - 7x + 6 = 0
f, x4 - 4x3 + 12x - 9 = 0
g, x5- 5x3 + 4x = 0
h, x4 - 4x3 + 3x2 + 4x - 4 = 0
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
Đúng 0
Bình luận (0)
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
Đúng 0
Bình luận (0)
Tìm x :
a ) 2(x2+8x+16) -x2+4 = 0
b ) x3-9x2+19x-11=0
Bài 6: Giải các phương trình sau:2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) x2 – 2x + 1 015) 1 + 3x + 3x2 + x3 0
Đọc tiếp
Bài 6: Giải các phương trình sau:
2) |
3) |
4) |
5) |
6) |
7) |
8)
9)
10)
11)
12)
13)
14) x2 – 2x + 1 = 0
15) 1 + 3x + 3x2 + x3 = 0
4) Ta có: \(\dfrac{2x-5}{5}-\dfrac{x+3}{3}=\dfrac{2-3x}{2}-x-2\)
\(\Leftrightarrow\dfrac{6\left(2x-5\right)}{30}-\dfrac{10\left(x+3\right)}{30}=\dfrac{15\left(2-3x\right)}{30}-\dfrac{30\left(x+2\right)}{30}\)
\(\Leftrightarrow12x-30-10x-30=30-45x-30x-60\)
\(\Leftrightarrow-22x-60=-75x-30\)
\(\Leftrightarrow-22x+75x=-30+60\)
\(\Leftrightarrow53x=30\)
\(\Leftrightarrow x=\dfrac{30}{53}\)
Vậy: \(S=\left\{\dfrac{30}{53}\right\}\)
5) Ta có: \(\dfrac{5x-3}{6}-\dfrac{7x-1}{4}=5\)
\(\Leftrightarrow\dfrac{2\left(5x-3\right)}{12}-\dfrac{3\left(7x-1\right)}{12}=\dfrac{60}{12}\)
\(\Leftrightarrow10x-6-21x+3=60\)
\(\Leftrightarrow-11x-3=60\)
\(\Leftrightarrow-11x=63\)
\(\Leftrightarrow x=-\dfrac{63}{11}\)
Vậy: \(S=\left\{-\dfrac{63}{11}\right\}\)
Đúng 1
Bình luận (1)
`9,x^3+x^2-2=0`
`x^3-x^2+2x^2-2=0`
`<=>x^2(x-1)+2(x-1)(x+1)=0`
`<=>(x-1)(x^2+2x+2)=0`
`<=>x=1`
`14,x^2-2x+1=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
`15,x^3+3x^2+3x+1=0`
`<=>(x+1)^3=0`
`<=>x+1=0`
`<=>x=-1`
Đúng 2
Bình luận (0)
Bài 6: Giải các phương trình sau:1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) x2 – 2x + 1 015) 1 + 3x + 3x2 + x3 0
Đọc tiếp
Bài 6: Giải các phương trình sau:
1) |
2) |
3) |
4) |
5) |
6) |
7) |
8)
9)
10)
11)
12)
13)
14) x2 – 2x + 1 = 0
15) 1 + 3x + 3x2 + x3 = 0
Bài 6:
1) Ta có: \(2x\left(x-5\right)-\left(x+3\right)^2=3x-x\left(5-x\right)\)
\(\Leftrightarrow2x^2-10x-\left(x^2+6x+9\right)=3x-5x+x^2\)
\(\Leftrightarrow2x^2-10x-x^2-6x-9-3x+5x-x^2=0\)
\(\Leftrightarrow-14x-9=0\)
\(\Leftrightarrow-14x=9\)
\(\Leftrightarrow x=-\dfrac{9}{14}\)
Vậy: \(S=\left\{-\dfrac{9}{14}\right\}\)
Đúng 5
Bình luận (0)
`1)2x(x-5)-(x+3)^2=3x-x(5-x)`
`<=>2x^2-10x-x^2-6x-9=3x-5x+x^2`
`<=>x^2-16x-9=x^2-2x`
`<=>14x=-9`
`<=>x=-9/14`
Đúng 3
Bình luận (0)