#)Giải :

a)\(\Delta ABC\)vuông tại A (gt) \(\Rightarrow\widehat{BAD}+\widehat{DAC}=90^o\left(1\right)\)

\(\Delta HAD\)vuông tại H (gt)\(\Rightarrow\widehat{HDA}+\widehat{HAD}=90^o\left(2\right)\)

Vì AD là tia phân giác của \(\widehat{HAC}\Rightarrow\)\(\widehat{HAD}=\widehat{DAC}\left(3\right)\)

Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{BAD}=\widehat{DAC}\)

\(\Rightarrow\Delta ABD\)cân tại A

b) Từ cmt \(\Rightarrow AB=BD\)(tính chất của tam giác cân)

Đặt \(AB=BD=x\)

Áp dụng hệ thức lượng trong tam giác vuông ABC 

\(\Rightarrow AB^2=HB.HC\)

Hay \(x^2=\left(x-6\right)25\)

\(\Rightarrow x^2-25+150=0\)

\(\Rightarrow\left(x-10\right)\left(x-15\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-10=0\\x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\x=15\end{cases}}}\)

Vậy AB = 10 hoặc AB = 15

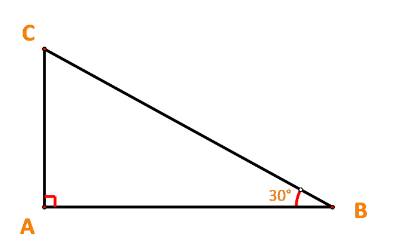
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)

\(\overrightarrow {BA} .\overrightarrow {BC}  = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)

\(\overrightarrow {CA} .\overrightarrow {CB}  = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)

1.a,

Vi:\(\Delta ABC\)co \(\widehat{A}=60\)do nen \(\Delta ABC\)la tam giac deu(dinh nghia)

\(\Rightarrow\widehat{ABC}=\widehat{BCA}=60\)do(Dinh ly Py-ta-go)

Ma BD,CE lan luot la phan giac cua \(\widehat{ABC}\)va\(\widehat{ACB}\)nen   \(\widehat{B_1}=\widehat{C_1}=\widehat{B_2}=\widehat{C_2}\)

\(\Delta BOC\)co :\(\widehat{B_2}=\widehat{C_2}\)

\(\Rightarrow\Delta OBC\)la tam giac can( tinh chat)

\(\Rightarrow OB=OC\left(dinhnghia\right)\)

xet \(\Delta EOB\)va \(\Delta DOC\)co :

\(\widehat{E_1}=\widehat{C_1}\)

\(\widehat{O_1}=\widehat{O_2}\)(doi dinh)

OB\(=\)OC(c/m tren)

\(\Rightarrow\Delta OEB=\Delta ODC\left(g.c.g\right)\)

\(\Rightarrow OE=OD\)(2  canh tuong ung)

\(\Rightarrow\Delta EOD\)la tam giac can tai O (dpcm)

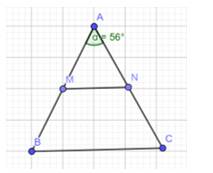
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)

Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)

b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )

Mà M, N là trung điểm của AB, AC

Nên AM = AN

Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A

\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)

c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)

Mà chúng ở vị trí đồng vị nên MN⫽BC