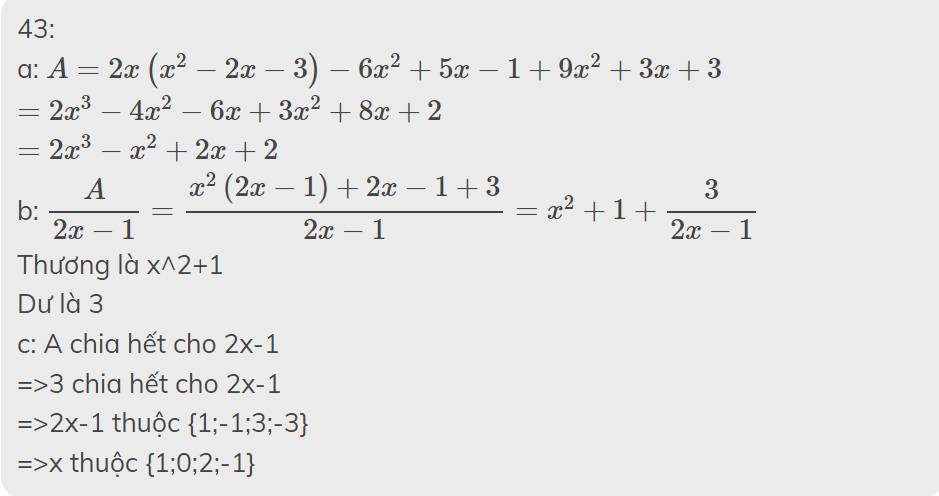Ta có:

3x²-5x-7=3x²-9x+4x-12+5=3x(x-3)+4(x-3)+5=(x-3)(3x+4)+5

Nhận thấy: (x-3)(3x+4) luôn chia hết cho x-3 với mọi x

=> Để biểu thức nguyên thì 5 phải chia hết cho x-3

=> x-3 là ước của 5 => x-3=(-5,-1,1,5)

=> x thuộc (-2; 2; 4; 8)

a) Cho x² - x + 5=0 =>x={ \(\frac{1}{2}+\frac{\sqrt{19}}{2}i;\frac{1}{2}-\frac{\sqrt{19}}{2}i\) }

Thay giá trị của x là \(\frac{1}{2}+\frac{\sqrt{19}}{2}i\)hoặc \(\frac{1}{2}-\frac{\sqrt{19}}{2}i\) vừa tìm được vào x⁴ - x³ + 6x²- x sẽ luôn được kết quả là -5

=>-5 +a=0 => a=5

b) Cho x+2=0 => x=-2

Thay giá trị của x vào biểu thức 2x³ -  3x² + x sẽ được kết quả là -30

=> -30 + a=0 => a=30 

a) Cho 3n +1 =0 => n= \(\frac{-1}{3}\)

Thay n= \(\frac{-1}{3}\)vào biểu thức 3n³ + 10n² -5 sẽ được kết quả -4

Vậy n = -4

b) Cho n-1=0 => n=1

 Thay n=1 vào biểu thức 10n² + n -10 sẽ được kết quả là 1

Vậy n = 1

2x²+3x+2=2x²+2x+x+2=2x(x+1)+(x+2)

Vì 2x(x+1) chia hết cho x+1

=> x+2 chia hết cho x+1

Ta có: x+2=x+1+1

x nguyên => x+1 nguyên => x+1 thuộc Ư (1)={-1;1}
Với x+1=1 => x=0

Với x+1=-1 => x=-2

Vậy x={0;-2} thì 2x²+3x+2 chia hết cho x+1

Ta có : 2.x²+3x+2 \(⋮\)x+1

=) [ 2.x²+3x+2 - ( x + 1 ) ] \(⋮\)x+1

=) [ 2.x²+3x+2 - 3( x + 1 ) ]  \(⋮\)x+1

=) [ 2.x²+3x+2 - (3x + 3 ) ]  \(⋮\)x+1

=)  2.x²+3x+2 - 3x - 3   \(⋮\)x+1

\(2x^2+3x+2⋮x+1\)

\(\Rightarrow2x^2+2x+x+2⋮x+1\)

\(\Rightarrow2x\left(x+1\right)+\left(x+1\right)+1⋮x+1\)

\(\Rightarrow1⋮x+1\)\(\Rightarrow x+1\inƯ\left(1\right)=\left\{\pm1\right\}\)

\(\Rightarrow\hept{\begin{cases}x+1=1\\x+1=-1\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=0\\x=-2\end{cases}}\)

2x²+3x+2=2x²+2x+x+2=2x(x+1)+(x+2)

Vì 2x(x+1) chia hết cho x+1

=> x+2 chia hết cho x+1

Ta có: x+2=x+1+1

x nguyên => x+1 nguyên => x+1 thuộc Ư (1)={-1;1}
Với x+1=1 => x=0

Với x+1=-1 => x=-2

Vậy x={0;-2} thì 2x²+3x+2 chia hết cho x+1

=>3x+15-55 chia hết cho x+5

=> 3(x+5) -55 chia hết cho x+5

vì 3(x+5) chia hết cho x+5 nên 55 cũng chhia hết cho x+5

=> x+5 là ước của 55

=> x+5={1,-1,5,-5,11,-11,55,-55}

xét x+5 =....( đoạn này bạn tự làm nhé)

b) => 3x-12+4 chia hết cho x-4

=> 3(x-4) +4 chia hết cho x-4

vì 3(x-4) chia hết cho x-4 nên 4 chia hết cho x-4

=> x-4 là ước của 4

=> x-4={-1,1,-2,2,-4,4}

xét x-4=.....(bn xét lần lượt nha^^)

Ta có : \(2x^2+3x+2=\left(2x^2+2x\right)+\left(x+1\right)+1\)

\(=2x\left(x+1\right)+\left(x+1\right)+1=\left(x+1\right)\left(2x+1\right)+1\)

Để \(\left(2x^2+3x+2\right)⋮\left(x+1\right)\)

thì \(1⋮x+1\) hay \(x+1\inƯ\left(1\right)\)

\(\Rightarrow x+1\in\left\{-1,1\right\}\)

\(\Leftrightarrow x\in\left\{-2,0\right\}\)

Vậy : \(x\in\left\{-2,0\right\}\) để \(\left(2x^2+3x+2\right)⋮\left(x+1\right)\)

3x+2\(⋮\)x-1

<=> 3x - 3 + 5 \(⋮\)x - 1

Vì 3x - 3 \(⋮\)x - 1 mà  3x - 3 + 5 \(⋮\)x - 1 nên:

=> 5 \(⋮\)x - 1

x - 1 \(\in\){ -5;-1;1;5}

=> x \(\in\){ -4;0;2;6}

Vậy x = { -4;0;2;6}