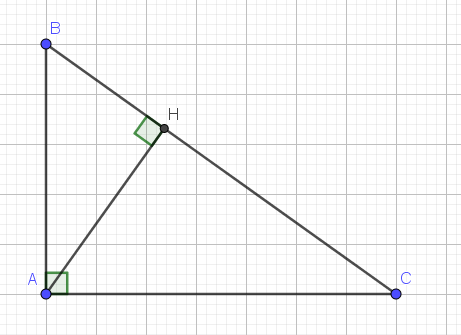
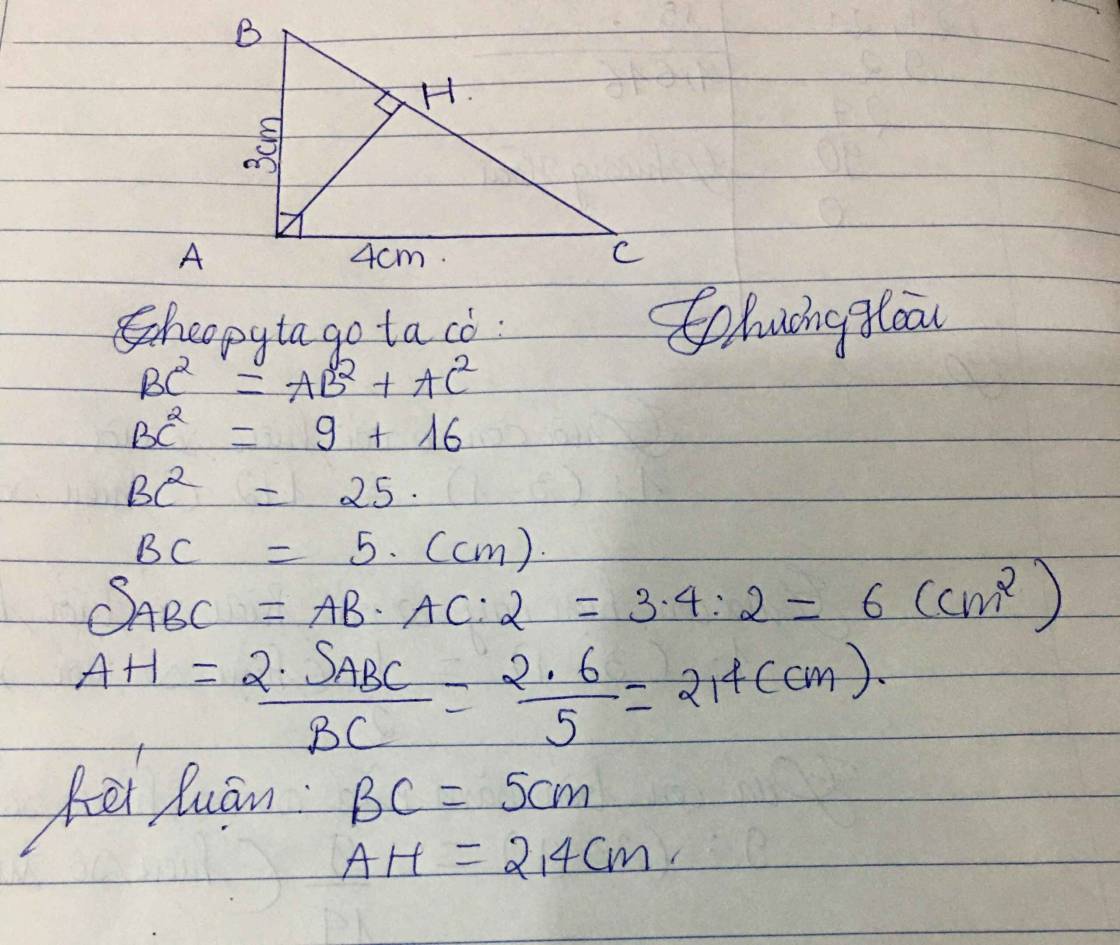Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm; BC = 5cm. a/ Tính AC, AH, HB, HC. b/ Tính các tỉ số lượng giác của góc B và tính góc C. c/ Vẽ HM vuông góc AB tại M; vẽ HN vuông góc AC tại N. Chứng minh: AM. AB = AN. AC.

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AB 9cm, BC 15cm. Tính BH, HC b) Biết BH 1cm, HC 3cm. Tính AB, AC c) Biết AB 6cm, AC 8cm. Tính AH, BCBài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, BH 2,4cm a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc BBài 3: Cho tam giác ABC có BC 9cm, góc B 60 độ, góc C 40 độ, đường cao AH. Tính AH, AB, AC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB= 9cm, BC= 15cm. Tính BH, HC
b) Biết BH= 1cm, HC= 3cm. Tính AB, AC
c) Biết AB= 6cm, AC= 8cm. Tính AH, BC
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB= 3cm, BH= 2,4cm
a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc B
Bài 3: Cho tam giác ABC có BC= 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC3cm ,BC6cm . Tính độ dài các đoạn thẳng AB, AC .2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC3:7 , AH42cm.Tính độ dài BH , CH3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB21cm,AC28cm .Tính HD
Đọc tiếp
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC=3cm ,BC=6cm . Tính độ dài các đoạn thẳng AB, AC .
2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=3:7 , AH=42cm.Tính độ dài BH , CH
3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH=9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC
4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB=21cm,AC=28cm .Tính HD
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB12CM,Ac5cm.tính BH,CHCâu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB18cm,BH6cm.tính đô dài các cạnh AB,ACCâu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac4cm,a.tinh bcb:kẻ đường cao ah,tính bhCâu 4:cho tam giác ABC Vuông tại A,biết ab4cm,đường cao ah2cm.Tính các góc và các cạnh còn lại của tam giác
Đọc tiếp
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB=12CM,Ac=5cm.tính BH,CH
Câu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB=18cm,BH=6cm.tính đô dài các cạnh AB,AC
Câu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac=4cm,
a.tinh bc
b:kẻ đường cao ah,tính bh
Câu 4:cho tam giác ABC Vuông tại A,biết ab=4cm,đường cao ah=2cm.Tính các góc và các cạnh còn lại của tam giác
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
Đúng 0
Bình luận (0)
Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=3cm, AC=4cm. Tính AH, BH
xét △ABC vuông tại A
BC2= AB2+ AC2
BC2= 32+ 42
BC2= 25
BC=\(\sqrt{25}=5\)
Xét △ABC vuông tại A, có AH là đường cao
AB.AC=AH.BC
3.4=AH.5
AH= \(\dfrac{3.4}{5}=2,4\)
Xét △ ABC vuông tại A
AB2= BH.BC
32= BH. 5
BH= 1,8
Đúng 2
Bình luận (0)
tham khảo ở đây
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-vuong-tai-a-duong-cao-ah-biet-ab-3cm-ac-4cm-tinh-do-dai-cac-canh-bc-ah-va-so-do-goc-acb-lam-tron-den-do.1482642245232
tính BH
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại ta có
AB2=BC.BH \(\Leftrightarrow\) BH=AB2/BC \(\Leftrightarrow\) BH=9/5
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , Đường cao AH; biết HB = 3cm , HC = 4cm . Tính AB, AH
Lời giải:
a.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=3.4=12$
$\Rightarrow AH=\sqrt{12}=2\sqrt{3}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=3(3+4)=21$
$\Rightarrow AB=\sqrt{21}$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, AC 4cm. Tính độ dài đường cao AH, tính
c
o
s
A
C
B
^
và chu vi tam giác ABH. A. AH 2,8 cm;
c
o
s
A
C
B
^
3
5
B. AH 2,4 cm; ...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính c o s A C B ^ và chu vi tam giác ABH.
A. AH = 2,8 cm; c o s A C B ^ = 3 5
B. AH = 2,4 cm; c o s A C B ^ = 4 5
C. AH = 2,5 cm; c o s A C B ^ = 3 4
D. AH = 1,8 cm; c o s A C B ^ = 2 3
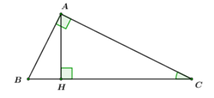
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH biết AB=6cm, BH=3cm. Tính AH,BC,AC
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BC=\dfrac{AB^2}{BH}=12\left(cm\right)\)
Áp dụng định lý Pitago:
\(AC=\sqrt{BC^2-AB^2}=6\sqrt{3}\left(cm\right)\)
Hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=3\sqrt[]{3}\left(cm\right)\)
Đúng 2
Bình luận (0)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BC=\dfrac{6^2}{3}=12\left(cm\right)\)
Ta có:BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=12-3=9(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=3\cdot9=27\)
hay \(AH=3\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=12^2-3^2=135\)
hay \(AC=3\sqrt{15}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Cho tam giác ABC vuông tại A, đường cao AH.
Biết AB = 8cm, BH = 4cm. Tính: BC, HC, AH.
b) Cho tam giác ABC vuông tại A, đường cao AH.
Biết AB = 6cm, BH = 3cm. Tính: BC, HC, AH.
a: \(AH=4\sqrt{3}\left(cm\right)\)
HC=12cm
BC=16cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Đường phân giác góc C cắt AH tại M, cắt AB tại N. Biết: AB=3cm, AC=4cm. Tính HC, BC
+xét tam giác ABC vuông tại A:
=> BC2=AC2+AB2(Định lý pytago)
hay BC2=16+9
BC2= 25
Mà BC>0
=> BC=5(cm)
+xét tam giác ABH vuông tại H và tam giác ABC vuông tại A có:
GÓC B: góc chung
góc A=góc H=90độ (tam giác ABC vuông tại A,AH:đường cao)
=> tam giác ABH đồng dạng với tam giác ABC(góc-góc)
=> BH/AB=BA/BC(các cặp cạnh tương ứng tỉ lệ)
hay BH/3=3/5
=> BH=1,8(cm)
=> HC=5-1,8=4,8(cm)
p/s: mình thấy sai sai , vì sao có dữ liệu phân giác góc C mà lại không dùng đến(bạn tham khảo thử bài mình thôi nhé).Các góc,đồng dạng,độ , bạn cùng kí hiệu.Thông cảm hình mình vẽ hơi tởm=))
Đúng 1
Bình luận (0)
1, Cho tam giác ABC vuông tại A,đường cao AH
a, Cho biêt AB=3cm,BC=5cm.Tính độ dài đoạn thẳng BH,CH,AH và AC
b,Cho biết AH=60cm,CH=144cm.Tính độ dài đoạn thẳng AB,AC,BC và BH
2, Cho tam giác ABC vuông tại A, đường cao AH
Cho biết \(\dfrac{AB}{AC}\)=\(\dfrac{5}{6}\) và BC=122cm.Tính độ dài các đoạn thẳng BH,CH
Bài 2:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{25}{36}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: HB+HC=BC
\(\Leftrightarrow HC\cdot\dfrac{61}{36}=122\)
\(\Leftrightarrow HC=72\left(cm\right)\)
hay HB=50(cm)
Đúng 1
Bình luận (0)