Số nghiệm thực của phương trình \(x^4-9x^2+24x-16=0\)

Những câu hỏi liên quan
Giải các phương trình:
a) $x^4-9x^2+24x-16 = 0;$
b) $x^4 = 6x^2+12x+8;$
c) $x^4 = 4x+1;$
d) $x^3-x^2-x=\dfrac 13$.
\(x^4-9x^2+24x-16=\)\(0\)
\(\Leftrightarrow x^4-\left(9x^2-24x+16\right)=0\)
\(\Leftrightarrow x^4-\left(3x-4\right)^2=0\)
\(\Leftrightarrow\left(x^2+3x-4\right)\left(x^2-3x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]=0\)
Vì \(\left(x-\frac{3}{2}\right)^2+\frac{7}{4}>0\forall x\)nên:
\(\left(x+4\right)\left(x-1\right)=0:\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)
Vậy phương trình có tập nghiệm \(S=\left\{1;-4\right\}\)
\(x^4=6x^2+12x+\)\(8\)
\(\Leftrightarrow x^4-2x^2+1=4x^2+12x+9\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow|x^2-1|=|2x+3|\)\(|\)
xét các trường hợp:
- Trường hợp 1:
\(x^2-1=2x+3\)
\(\Leftrightarrow x^2-1-2x-3=0\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-5=0\Leftrightarrow\left(x-1\right)^2=5\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=\sqrt{5}\\x-1=-\sqrt{5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{cases}}}\)
-Trường hợp 2:
\(x^2-1=-2x-3\)
\(\Leftrightarrow x^2-1+2x+3=0\)
\(\Leftrightarrow x^2+2x+2=0\)
\(\Leftrightarrow\left(x+1\right)^2+1=0\)
\(\Leftrightarrow\left(x+1\right)^2=-1\left(vn\right)\)(vô nghiệm)
Vậy phương trình có tập nghiệm: \(S=\left\{1\pm\sqrt{5}\right\}\)
\(x^4=4x+1\)
\(\Leftrightarrow x^4+2x^2+1=2x^2+4x+2\)
\(\Leftrightarrow\left(x^2+1\right)^2=2\left(x+1\right)^2\)
\(\Leftrightarrow|x^2+1|=|x\sqrt{2}+\sqrt{2}|\)
Xét các trường hợp sau:
-Trường hợp 1:
\(x^2+1=x\sqrt{2}+\sqrt{2}\)
\(\Leftrightarrow x^2+1-x\sqrt{2}-\sqrt{2}=0\)
\(\Leftrightarrow\left(x^2-2x.\frac{\sqrt{2}}{2}+\frac{1}{2}\right)-\frac{2\sqrt{2}-1}{2}=0\)
\(\Leftrightarrow\left(x-\frac{1}{\sqrt{2}}\right)^2=\frac{2\sqrt{2}-1}{2}\)
Vì \(\frac{2\sqrt{2}-1}{2}>0\)nên:
\(\left|x-\frac{1}{\sqrt{2}}\right|=\left|\sqrt{\frac{2\sqrt{2}-1}{2}}\right|\)
Lại xét các trường hợp:
+Trường hợp 1.1:
\(x-\frac{1}{\sqrt{2}}=\frac{\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\)\(\Leftrightarrow x=\frac{\sqrt{2\sqrt{2}-1}+1}{\sqrt{2}}\)
+Trường hợp 1.2:
\(x-\frac{1}{\sqrt{2}}=\frac{\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\Leftrightarrow x=\frac{1-\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\)
-Trường hợp 2:
\(x^2+1=-x\sqrt{2}-\sqrt{2}\)(2)
\(\Leftrightarrow x^2+1+x\sqrt{2}+\sqrt{2}=0\)
\(\Leftrightarrow\left(x^2+2x.\frac{\sqrt{2}}{2}+\frac{1}{2}\right)+\frac{1+2\sqrt{2}}{2}=0\)
\(\Leftrightarrow\left(x+\frac{1}{\sqrt{2}}\right)^2=\frac{-1-2\sqrt{2}}{2}\)(vô nghiệm)
Do đó phương trình (2) vô nghiệm.
Vậy phương trình có tập nghiệm : \(S=\left\{\frac{1\pm\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\right\}\)
Xem thêm câu trả lời
giải phương trình \(x^4-9x^3+24x^2-27x+9=0\)
nhận thấy x = 0 không là nghiệm của phương trình
Chia 2 vế phương trình cho x2, ta được :
\(x^2-9x+24-\frac{27}{x}+\frac{9}{x^2}=0\) ( 1 )
đặt \(t=x+\frac{3}{x}\)
( 1 ) \(\Leftrightarrow\left(x+\frac{3}{x}\right)^2-9\left(x+\frac{3}{x}\right)+18=0\)
\(\Leftrightarrow t^2-9t+18=0\Leftrightarrow\left(t-6\right)\left(t-3\right)=0\Leftrightarrow\orbr{\begin{cases}t=6\\t=3\end{cases}}\)
Khi đó : \(\orbr{\begin{cases}x+\frac{3}{x}=6\Leftrightarrow x=3\pm\sqrt{6}\\x+\frac{3}{x}=3\Leftrightarrow x\in\varnothing\end{cases}}\)
Cho phương trình
y
x
3
-
6
x
2
+
9
x
-
2
và các phát biểu sau:(1) x 0 là nghiệm duy nhất của phương trình(2) Phương trình có nghiệm dương (3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1(4) Phương trình trên có tổng 2 nghiệm là:
-
log...
Đọc tiếp
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Giải phương trình:
a) x4 - 10x3 + 25x2 - 36 = 0
b) x4 - 9x2 - 24x - 16 = 0
a. \(x^4-10x^3+25x^2-36=0\)
=> \(x^3\left(x-3\right)-7x^2\left(x-3\right)+4x\left(x-3\right)+12\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x^3-7x^2+4x+12\right)=0\)
=>\(\left(x-3\right)\left[x^2\left(x-2\right)-5x\left(x-2\right)-6\left(x-2\right)\right]=0\)=> \(\left(x-3\right)\left(x-2\right)\left(x^2-5x-6\right)=0\)
=> \(\left(x-3\right)\left(x-2\right)\left(x+1\right)\left(x-6\right)=0\)
=>\(\left[\begin{matrix}x=3\\x=2\\x=-1\\x=6\end{matrix}\right.\)
b) \(x^4\) - \(^{9x^2}\) - 24x - 16 = 0
=> \(x^3\left(x-4\right)+4x^2\left(x-4\right)+7x\left(x-4\right)+4\left(x-4\right)=0\)=>\(\left(x-4\right)\left(x^3+4x^2+7x+4\right)=0\)
=> \(\left(x-4\right)\left[x^2\left(x+1\right)+3x\left(x+1\right)+4\left(x+1\right)\right]=0\)=>\(\left(x-4\right)\left(x+1\right)\left(x^2+3x+4\right)=0\)
=> \(\left(x-4\right)\left(x+1\right)=0\) (vì x^2 + 3x + 4> 0)
=>\(\left[\begin{matrix}x=4\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a,pt\(\Leftrightarrow\left(x^4-10x^3+25x\right)-36=0\)\(\Leftrightarrow\left(x^2-5x\right)^2-36=0\)
\(\Leftrightarrow\left(x^2-5x-6\right)\left(x^2-5x+6\right)=0\)\(\Leftrightarrow\left[\begin{matrix}x^2-5x-6=0\\x^2-5x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}\left(x+1\right)\left(x-6\right)=0\\\left(x-2\right)\left(x-3\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[\begin{matrix}x=-1,x=6\\x=2,x=3\end{matrix}\right.\)
vậy pt có 4 nghiệm x=(-1,6,2,3)
Đúng 0
Bình luận (0)
pt\(\Leftrightarrow x^4-\left(9x^2+24x+16\right)=0\)\(\Leftrightarrow\left(x^2\right)^2-\left(3x+4\right)^2=0\)\(\Leftrightarrow\left(x^2-3x-4\right)\left(x^2+3x+4\right)=0\)\(\Leftrightarrow\left[\begin{matrix}x^2-3x-4=0\\x^2+3X+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}\left(x-4\right)\left(x+1\right)=0\\x^2+3x+4>0\end{matrix}\right.\)\(\Leftrightarrow x=4,x=-1\)
vậy pt có nghiệm x=(4,-1)
Đúng 0
Bình luận (0)
Bài 4: a. Cho phương trình: x ^ 2 - 9x + 16 = 0 có hai nghiệm dương phân biệt X_{1} X_{2} . Không giải phương trình, hãy tính giá trị của biểu thức T = (x_{1} * sqrt(x_{2}) + x_{2} * sqrt(x_{1}))/(x_{1} ^ 2 + x_{2} ^ 2)
\(T=\dfrac{\left(x1\cdot\sqrt{x_2}+x_2\cdot\sqrt{x_1}\right)}{x1^2+x_2^2}\)
\(=\dfrac{\sqrt{x_1\cdot x_2}\left(\sqrt{x_1}+\sqrt{x_2}\right)}{\left(x_1+x_2\right)^2-2x_1x_2}\)
\(=\dfrac{4\cdot\sqrt{x_1+x_2+2\sqrt{x_1x_2}}}{9^2-2\cdot16}=\dfrac{4\cdot\sqrt{9+2\cdot4}}{81-32}\)
\(=\dfrac{4\sqrt{17}}{49}\)
Đúng 0
Bình luận (0)
Tìm giá trị thực của tham số m để phương trình
9
x
-
2
.
3
x
+
1
+
m
0
có 2 nghiệm thực
x
1
;
x
2
thỏa mãn
x
1
+
x
2...
Đọc tiếp
Tìm giá trị thực của tham số m để phương trình 9 x - 2 . 3 x + 1 + m = 0 có 2 nghiệm thực x 1 ; x 2 thỏa mãn x 1 + x 2 = 1
A. m=3
B.m=6
C. m=1
D. m=-3
Số nghiệm của phương trình 9x + 2(x – 2).3x + 2x – 5 = 0 là:
A. 0.
B. 1.
C. 2.
D. Vô số.
Đáp án B.
Đặt 3x = t > 0.
Phương trình <=> t2 + 2(x – 2)t + 2x – 5 = 0
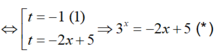
Có f(x) = 3x là hàm số đồng biến trên ℝ
g(x) = –2x + 5 là hàm số nghịch biến trên ℝ
=> Phương trình (*) ó f(x) = g(x) có nhiều nhất l nghiệm
Có f(1) = g(1) => x = 1 là nghiệm của phương trình.
Đúng 0
Bình luận (0)
Số nghiệm của phương trình
9
x
+
2
(
x
−
2
)
.3
x
+
2
x
−
5
0
là: A. 0. B. 1 C. 2. D. Vô số
Đọc tiếp
Số nghiệm của phương trình 9 x + 2 ( x − 2 ) .3 x + 2 x − 5 = 0 là:
A. 0.
B. 1
C. 2.
D. Vô số
Đáp án B.
Đặt 3 x = t > 0 .
Phương trình
⇔ t 2 + 2 ( x − 2 ) t + 2 x − 5 = 0 ⇔ t = − 1 ( 1 ) t = − 2 x + 5 ⇒ 3 x = − 2 x + 5 (*)
Có f ( x ) = 3 x là hàm số đồng biến trên R
g ( x ) = − 2 x + 5 là hàm số nghịch biến trên R
Phương trình (*) ⇔ f ( x ) = g ( x ) có nhiều nhất l nghiệm
Có f ( 1 ) = g ( 1 ) ⇒ x = 1 là nghiệm của phương trình
Đúng 0
Bình luận (0)
Số nghiệm của phương trình 9 x + 2 ( x − 2 ) .3 x + 2 x − 5 = 0 là:
A. 0
B. 1
C. 2
D. Vô số
















