Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
#: các bn giúp mk na, thanks yoo nhìu nhìu
Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
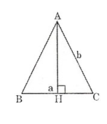
Gọi h là chiều cao của tam giác cân.
Theo định lí Pitago ta có:
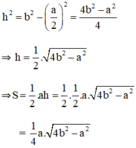
Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.
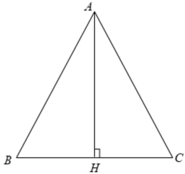
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC = 1/2BC = a/2
Khi đó ta có: S A B C = 1 2 A H . B C = 1 2 . a . A H
Áp dụng định lý Py – to – go ta có:
A C 2 = A H 2 + H C 2 ⇒ A H = A C 2 - H C 2
Khi đó SABC = 1/2AH.BC
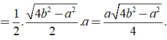
Do đó diện tích của tam giác đều các cạnh bằng a là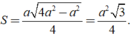
Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.
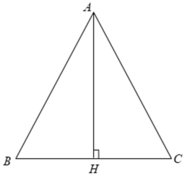
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC = 1/2BC = a/2
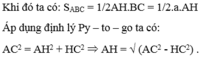
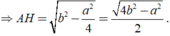
Khi đó SABC = 1/2AH.BC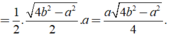
Do đó diện tích của tam giác đều các cạnh bằng a là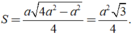
Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b ?
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
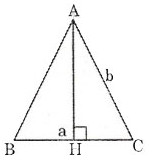
Theo định lý Pitago ta có
h2 = b2 -  =
= 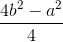
h = 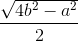
Nên S =  ah =
ah =  a.
a. 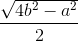 =
=  a.
a. 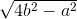 .
.
Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
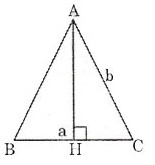
Theo định lý Pitago ta có
h2 = b2 –  =
= 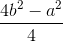
h = 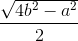
Nên S =  ah =
ah =  a.
a. 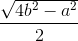 =
=  a.
a. 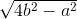
Tự vẽ hình nhé bạn
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
Theo định lý Pitago ta có :
\(h^2=b^2-\left(\frac{a}{b}\right)^2=\frac{4b^2-a^2}{4}\)
\(h=\frac{\sqrt{4b^2-a^2}}{2}\)
\(\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a.\frac{\sqrt{4b^2-a^2}}{2}=\frac{1}{4}a.\sqrt{4b^2-a^2}\)
Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằnng b
Tính diện tích của 1 tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
\(h=\sqrt{b^2-\frac{a^2}{4}}=\frac{\sqrt{4b^2-a^2}}{2}\)
\(S=\frac{1}{2}.a.h=\frac{1}{2}.a.\frac{\sqrt{4b^2-a^2}}{2}=\frac{a\sqrt{4b^2-a^2}}{4}\)
1, góc ở đỉnh của một tam giác cân bằng 78 độ , cạnh đáy dài 28,5cm. Tính cạnh bên và diện tích tam giác
2 ,cạnh bên của một tam giác cân dài 17,2cm. góc ở đáy của tam giác cân là 46 độ. Tính cạnh đáy và diện tích tam giác
. Giúp mình với ạ!! Cảm ơn nhìu ạ
1 Tam giác đều có độ dài cạnh bằng 3cm. Tính diện tích tam giác.
2. Tam giác cân có cạnh bên bằng 8, cạnh đáy bằng 6. Tính diện tích tam giác.
3.Một hình thang có một đáy là 2x và các cạnh còn lại bằng x. Tìm x biết diện tích
hình thang bằng 6 căn 3 .
4.Một người đi xe đạp từ C đến Bvới vận tốc 15km/h. Hỏi đi được bao lâu thì người
đó cách đều hai điểm A và B?
5. Bạn Rô muốn treo một banner khuyến mãi dài 7m trước cửa hiệu. Có hai đinh treo
được đóng trên tường, tạo thành một đoạn thẳng song song mặt đất và có độ dài 10m.
Nếu muốn banner treo thấp hơn đoạn thẳng đó 1m thì độ dài hai dây treo phải là bao
nhiêu?
Câu 1:
Diện tích tam giác đều cạnh 3cm là:
\(S=\dfrac{3^2\cdot\sqrt{3}}{4}=\dfrac{9\sqrt{3}}{4}\left(cm^2\right)\)
Câu 2:
Nửa chu vi tam giác là:
\(P=\dfrac{C}{2}=\dfrac{8+8+6}{2}=\dfrac{22}{2}=11\left(cm\right)\)
Diện tích tam giác là:
\(S=\sqrt{P\cdot\left(P-A\right)\cdot\left(P-B\right)\cdot\left(P-C\right)}=\sqrt{11\cdot\left(11-8\right)^2\cdot\left(11-6\right)}\)
\(=\sqrt{11\cdot5\cdot9}=3\sqrt{55}\left(cm^2\right)\)