Bài 1: Cho tam giác ABC, có góc B=góc C. Tia phân giác BD, CE.
a, Chứng minh: BD=CE
b, Chứng minh: CD=BE
c, Chứng minh: ED// BC
Cho tam giác ABC (góc A=90). D thuộc BC sao cho BD=BA. Qua D kẻ đường thăng d vuông góc BC cắt tia đối của tia AB tại E. Chứng minh:
a)Tam giác BEC cân
b)ED cắt AC tại H. Chứng minh BH vuông góc EC
c)Tia Bx vuông góc BA, ED cắt Bx tại K
Chứng minh tam giác BHK cân.
Cho tam giác ABC vuông tại A, kẻ phân giác BD của góc b (D thuộc AC). Từ A kẻ AH vuông góc BD (H thuộc BD), tia AH cắt BC tại E.
A) Chứng minh : Tam giác BHA=tam giác BHE
B) Chứng minh : ED vuông góc BC
C) Kẻ AK vuông góc BC ( K thộc BC). Chứng minh : AE là tia phân giác của góc CAK
các bạn hãy giúp mình làm nha !
a) Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)(BH là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBHA=ΔBHE(cạnh góc vuông-góc nhọn kề)
b) Ta có: ΔBHA=ΔBHE(cmt)
nên BA=BE(hai cạnh tương ứng)
Xét ΔBAD và ΔBED có
BA=BE(cmt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔBAD=ΔBED(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
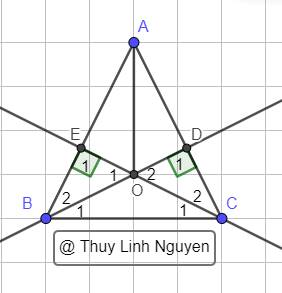
Cho tam giác ABC ( A < 90 độ), AB = AC.Kẻ CE vuông góc AB (E thuộc AB).Kẻ BD vuông góc AC,(D thuộc AC).Gọi O là giao điểm của BD và CE.
a)Chứng minh BD = CE
b)Chứng minh OE = OD và OB = OC
c)Chứng minh OA là phân giác BAC
Giúp mình nhé mình cần gấp
`a)`
Có `Delta ABC` cân tại `A(g t)`
`=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
Xét `Delta BEC` và `Delta CDB` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(BC-chung),(hat(EBC)=hat(DCB)(cmt)):}}`
`=>Delta BEC=Delta CDB(c.h-g.n)`
`=>CE=BD` ( 2 cạnh tương ứng )( dpcm )
`b)`
Có `Delta BEC=Delta CDB(cmt)`
`=>hat(C_1)=hat(B_1)` ( 2 góc tương ứng )
`=>Delta BOC` cân tại `O`
`=>OB=OC`(dpcm)
Xét `Delta OEB` và `Delta ODC` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(OB=OC(cmt)),(hat(O_1)=hat(O_2)(doi.di nh)):}}`
`=>Delta OEB=Delta ODC(c.h-g.n)`
`=>OE=OD`( 2 cạnh tương ứng )(dpcm)
`c)`
Có `Delta ABC` cân tại `A(g t)`
`=>AB=AC`
`=>A in ` trung trực của `Delta ABC(1)`
Có `OB=OC(cmt)`
`=>O in` trung trực của `Delta ABC(2)`
Từ `(1)` và `(2)=>OA` là trung trực `Delta ABC`
mà `Delta ABC` cân tại `A`
Nên `OA` là phân giác `hat(BAC)` (dpcm)
Bài 3: Cho tam giác ABC (AB < AC). Trên tia BA lấy điểm D sao cho BD = BC. Nối C với D. Tia phân giác của góc B cắt cạnh AC và CD theo thứ tự ở E và I.
a) Chứng minh DBID =DBIC b) Chứng minh ED = EC
c) Kẻ AH vuông góc với CD tại điểm H, chứng minh AH // BI.
a: Xét ΔBID và ΔBIC có
BD=BC
góc CBI=góc DBI
BI chung
Do đó: ΔBID=ΔBIC
b: Xét ΔBEC và ΔBED có
BE chung
góc EBC=góc EBD
BC=BD
Do đó: ΔBEC=ΔBED
=>ED=EC
c: ΔBCD cân tại B
mà BI là đường phân giác
nên BI vuông góc với CD
=>BI//AH
Bài 3: Cho tam giác ABC cân tại A. Tia phân giác của góc B cắt AC tại D và tia phân giác của góc C cắt AB tại E. a) Chứng minh rằng: EBDD EC= b) Chứng minh rằng: ADE cân c) Chứng minh rằng: ED // BC d) Gọi O là giao điểm của EC và BD. Chứng minh rằng: OBC cân
b: Xét ΔABD và ΔACE có
\(\widehat{BAD}\) chung
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
c: Xét ΔABC có
AE/AB=AD/AC
Do đó: DE//BC
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE.
a) Chứng minh AD = AE.
b) Chứng minh tam giác KBC cân.
c) Chứng minh AK là tia phân giác của góc A.
Cho tam giác ABC vuông tại A (AB<AC) Đường phân giác BD trên BC lấy E sao cho BE = AB a, chứng mình tam giác ADB = tam giác EDB b, tia ED cắt tia BA tại F chứng minh BC = BF c, chứng minh AE vuông góc với BD
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=góc BAD=90 độ
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
Do đó: ΔBEF=ΔBAC
=>BF=BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
BA=BE
=>B nằm trên trung trực của AE(1)
DA=DE
=>D nằm trên trung trực của AE(2)
Từ (1), (2) suy ra BD là đường trung trực của AE
=>BD vuông góc AE
Cho tam giác ABC cân tại A có góc A bằng 90 độ . Vẽ BD vuông góc tại D CE vuông góc AB tại E .Gọi I là giao điểm của BD và CE.
a)Chứng minh AD=AE
b)chứng minh AI là tia phân giác của góc BAC
c)Chứng minh DE song song với BC
d)Gọi M là trung điểm cạnh BC . Chứng minh ba điểm A,I,M thẳng hàng
ai giúp mình câu d với ạ. chỉ câu d thôi nha
Bài 1: Phân tích các biểu thức sau thành tích của hai đơn thức trong đó có một đơn thức là 20x5y2:
a, - 120x5y4 b, 60x6y2 c, -5x15y3
Bài 2: Điền đơn thức thích hợp vào chỗ trống:
a, 3x2y + ..........= 5 x2y b,........-2 x2 = -7 x2 c,......+.........+ x5 = x5
Bài 3: Thu gọn các đơn thức sau:
a, 5xy2(-3)y; b, 3/4 a2b3 . 2,5a; c, 1,5p.q.4p3.q2
d,2x2y.3xy2; e, 2xy.4/5x2y3.10xyz f,-10y2.(2xy)3.(-3x)2
Bài 4: Cho tam giác ABC vuông tại A (AC>AB). Gọi I là trung điểm của BC. Vẽ đường trung trực của cạnh BC cấtC tại D. Trên tia đối của tia AC lấy điểm E sao cho AE = AD. Gọi F là giao điểm của BE và đường thẳng AI. Chứng minh :
a, CD = BE; b, Góc BEC = 2. góc BEC
c, Tam giác AEF cân d, AC=BF
Bài 5: Cho tam giác ABC có góc A bằng 90o và BD là đường phân giác. Trên BC lấy điểm E sao cho BE = BA
a, Chứng minh AD = DE và BD là đường trung trực của đoạn thẳng AE
b, Kẻ AH vuông góc với BC. Chứng minh: AE là tia phân giác của góc HAC
c, Chứng minh AD<CD
d, Gọi tia Cx là tia đối của tia CB. Tia phân giác của góc Acx cắt đường thẳng BD tại K. Tính số đo góc BAK
Bài 6: Cho tam giác abc cân tại a, đường phân giác của góc b cắt ac tại M.
Kẻ me vuông góc với bc ( e thuộc bc). đường thẳng em cắt ba tại I
a, chứng minh tam giác abm = tam giác ebm
b, chứng minh bm là đường trung trực của ae
c, so sánh am và mc
d, chứng minh tam giác BCI cân